
【题目】如果抛物线C1的顶点在抛物线C2上,同时,抛物线C2的顶点在抛物线C1上,那么,我们称抛物线C1与抛物线C2互相依存.
(1)已知抛物线①:y=﹣2x2+4x+3与抛物线②:y=2x2+4x﹣1,请判断抛物线①与抛物线②是否互相依存,并说明理由.
(2)将抛物线C1:y=﹣2x2+4x+3沿x轴翻折,再向右平移m(m>0)个单位,得到抛物线C2,若抛物线C1与C2互相依存,求m的值.
(3)试问:如果对称轴不同的两条抛物线(二次函数图象)互相依存,那么它们的函数表达式中的二次项系数之间有什么数量关系?请说明理由.
【答案】(1)抛物线①与抛物线②相互依存(2)![]() (3)0
(3)0
【解析】
(1)根据两抛物线的关联依次判断即可;
(2)根据两抛物线关联的定义直接列式得出结论;
(3)设互相依存的一条抛物线为y1=a1(x﹣m1)2+n1
另一条抛物线为y2=a2(x﹣m2)2+n2,分别代入顶点,两式相加.
(1)由抛物线①知,y=﹣2x2+4x+3=﹣2(x﹣1)2+5,顶点坐标为(1,5),
把x=1代入抛物线②:y=2x2+4x﹣1,得y=5,
∴抛物线①的顶点在抛物线②上,
又由抛物线②知,y=2(x+1)2﹣3,顶点坐标为(﹣1,﹣3),
把x=﹣1代入抛物线①中,得,y=﹣3,
∴抛物线②的顶点在抛物线①上,
∴抛物线①与抛物线②相互依存.
(2)由抛物线①:y=﹣2(x﹣1)2+5,沿x轴翻折后为y=2(x﹣1)2﹣5,
设平移后的抛物线解析式为y=2(x﹣1﹣m)2﹣5,
把x=1,y=5代入得2(1﹣1﹣m)2﹣5=5,
∴m=±![]() ;
;
∵m>0,
∴m=![]() ,
,
∴当m=![]() 时,得到抛物线C2:y=2(x﹣1﹣
时,得到抛物线C2:y=2(x﹣1﹣![]() )2﹣5,顶点为(1+
)2﹣5,顶点为(1+![]() ,﹣5),
,﹣5),
把x=1+![]() 代入抛物线C1,得y=﹣5,
代入抛物线C1,得y=﹣5,
∴m=![]() ;
;
(3)它们的二次项系数互为相反数,理由如下:
设互相依存的一条抛物线为y1=a1(x﹣m1)2+n1,顶点为(m1,n1)
另一条抛物线为y2=a2(x﹣m2)2+n2,顶点为(m2,n2),其中m1≠m2,
∴把(m2,n2)代入y1,得n2=a1(m2﹣m1)2+n1,①
把(m1,n1)代入y2,得n1=a2(m1﹣m2)2+n2②
由①+②得,a1(m2﹣m1)2+a2(m1﹣m2)2=0
∵m1≠m2,
∴a1+a2=0.


科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(k﹣5)x+1﹣k=0(其中k为常数).
(1)求证无论k为何值,方程总有两个不相等实数根;
(2)已知函数y=x2+(k﹣5)x+1﹣k的图象不经过第三象限,求k的取值范围;
(3)若原方程的一个根大于3,另一个根小于3,求k的最大整数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
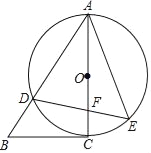
【题目】如图,AC是⊙O的直径,点D是⊙O 上一点,⊙O的切线CB与AD的延长线交于点B,点F是直径AC上一点,连接DF并延长交⊙O于点E,连接AE.
(1)求证:∠ABC=∠AED;
(2)连接BF,若AD=![]() ,AF=6,tan∠AED=
,AF=6,tan∠AED=![]() ,求BF的长.
,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商贸公司有![]() 、
、![]() 两种型号的商品需运出,这两种商品的体积和质量分别如下表所示:
两种型号的商品需运出,这两种商品的体积和质量分别如下表所示:
体积(立方米/件) | 质量(吨/件) | |
| 0.8 | 0.5 |
| 2 | 1 |
(1)已知一批商品有![]() 、
、![]() 两种型号,体积一共是20立方米,质量一共是10.5吨,求
两种型号,体积一共是20立方米,质量一共是10.5吨,求![]() 、
、![]() 两种型号商品各有几件?
两种型号商品各有几件?
(2)物资公司现有可供使用的货车每辆额定载重3.5吨,容积为6立方米,其收费方式有以下两种:
①按车收费:每辆车运输货物到目的地收费600元;
②按吨收费:每吨货物运输到目的地收费200元.
现要将(1)中商品一次或分批运输到目的地,如果两种收费方式可混合使用,商贸公司应如何选择运送、付费方式,使其所花运费最少,最少运费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋中装有4个只有颜色不同的球,其中1个黄球、1个蓝球、2个红球.
(1)任意摸出1个球,记下颜色后不放回,再任意摸出1个球.求两次摸出的球恰好都是红球的概率(要求画树状图或列表);
(2)现再将n个黄球放入布袋,搅匀后,使任意摸出1个球是黄球的概率为![]() ,求n的值.
,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来网约车十分流行,初三某班学生对“美团”和“滴滴”两家网约车公司各10名司机月收入进行了一项抽样调查,司机月收入(单位:千元)如图所示:

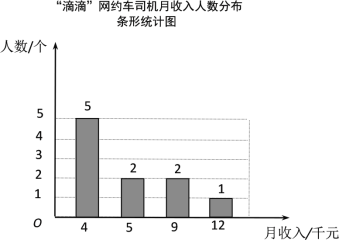
根据以上信息,整理分析数据如下:
平均月收入/千元 | 中位数/千元 | 众数/千元 | 方差/千元2 | |
“美团” | ① | 6 | 6 | 1.2 |
“滴滴” | 6 | ② | 4 | ③ |
(1)完成表格填空;
(2)若从两家公司中选择一家做网约车司机,你会选哪家公司,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(类比概念)三角形的内切圆是以三个内角的平分线的交点为圆心,以这点到三边的距离为半径的圆,则三角形可以称为圆的外切三角形,可以得出三角形的三边与该圆相切.以此类推,如图1,各边都和圆相切的四边形称为圆外切四边形
(性质探究)如图1,试探究圆外切四边形的ABCD两组对边AB,CD与BC,AD之间的数量关系
猜想结论: (要求用文字语言叙述)
写出证明过程(利用图1,写出已知、求证、证明)
(性质应用)
①初中学过的下列四边形中哪些是圆外切四边形 (填序号)
A:平行四边形:B:菱形:C:矩形;D:正方形
②如图2,圆外切四边形ABCD,且AB=12,CD=8,则四边形的周长是 .
③圆外切四边形的周长为48cm,相邻的三条边的比为5:4:7,求四边形各边的长.
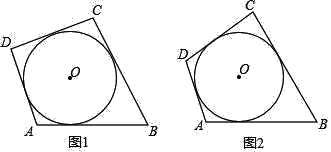
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD.

(1)求证:BD平分∠ABC;
(2) 当∠ODB=30°时,求证:BC=OD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E、F分别在BC、CD上移动,但A到EF的距离AH始终保持与AB长相等,问在E、F移动过程中:
(1)∠EAF的大小是否有变化?请说明理由.
(2)△ECF的周长是否有变化?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com