
【题目】某商贸公司有![]() 、
、![]() 两种型号的商品需运出,这两种商品的体积和质量分别如下表所示:
两种型号的商品需运出,这两种商品的体积和质量分别如下表所示:
体积(立方米/件) | 质量(吨/件) | |
| 0.8 | 0.5 |
| 2 | 1 |
(1)已知一批商品有![]() 、
、![]() 两种型号,体积一共是20立方米,质量一共是10.5吨,求
两种型号,体积一共是20立方米,质量一共是10.5吨,求![]() 、
、![]() 两种型号商品各有几件?
两种型号商品各有几件?
(2)物资公司现有可供使用的货车每辆额定载重3.5吨,容积为6立方米,其收费方式有以下两种:
①按车收费:每辆车运输货物到目的地收费600元;
②按吨收费:每吨货物运输到目的地收费200元.
现要将(1)中商品一次或分批运输到目的地,如果两种收费方式可混合使用,商贸公司应如何选择运送、付费方式,使其所花运费最少,最少运费是多少元?
【答案】(1)![]() 种型号商品有5件,
种型号商品有5件,![]() 种型号商品有8件;(2)先按车收费用3辆车运送18m3,再按吨收费运送1件B型产品,运费最少为2000元
种型号商品有8件;(2)先按车收费用3辆车运送18m3,再按吨收费运送1件B型产品,运费最少为2000元
【解析】
(1)设A、B两种型号商品各x件、y件,根据体积与质量列方程组求解即可;
(2)①按车付费=车辆数![]() 600;②按吨付费=10.5
600;②按吨付费=10.5![]() 200;③先按车付费,剩余的不满车的产品按吨付费,将三种付费进行比较.
200;③先按车付费,剩余的不满车的产品按吨付费,将三种付费进行比较.
(1))设A、B两种型号商品各x件、y件,
![]() ,
,
解得![]() ,
,
答:![]() 种型号商品有5件,
种型号商品有5件,![]() 种型号商品有8件;
种型号商品有8件;
(2)①按车收费:![]() (辆),
(辆),
但是车辆的容积![]() =18<20,3辆车不够,需要4辆车,
=18<20,3辆车不够,需要4辆车,![]() (元);
(元);
②按吨收费:200![]() 10.5=2100(元);
10.5=2100(元);
③先用车辆运送18m3,剩余1件B型产品,共付费3![]() 600+1
600+1![]() 200=2000(元),
200=2000(元),
∵2400>2100>2000,
∴先按车收费用3辆车运送18m3,再按吨收费运送1件B型产品,运费最少为2000元.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
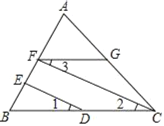
【题目】请你完成下面的证明:
已知:如图,∠GFB+∠B=180°,∠1=∠3,
求证:FC∥ED.
证明:∵∠GFB+∠B=180°
∴FG∥BC( )
∴∠3= ( ),
又∵∠1=∠3(已知)
∴∠1= (等量代换)
∴FC∥ED( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 是
是![]() 的直角三角形,
的直角三角形,![]() 的中点分别是点
的中点分别是点![]() 点
点![]() ,动点
,动点![]() 从点
从点![]() 出发,按箭头方向通过
出发,按箭头方向通过![]() 到
到![]() ;以
;以![]() 的速度运动,设
的速度运动,设![]() 点从
点从![]() 开始运动的距离为
开始运动的距离为![]() ,
,![]() 的面积为
的面积为![]() 试回答以下问题:
试回答以下问题:
(1)![]() 点从
点从![]() 出发到
出发到![]() 停止,写出
停止,写出![]() 与
与![]() 的函数关系式并写出
的函数关系式并写出![]() 的取值范围.
的取值范围.
(2)求出![]() 点从
点从![]() 出发后几秒时,
出发后几秒时,![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,AB∥OC,A(0,﹣4),B(a,b),C(c,0),并且a,c满足c=![]() +10.一动点P从点A出发,在线段AB上以每秒2个单位长度的速度向点B运动;动点Q从点O出发在线段OC上以每秒1个单位长度的速度向点C运动,点P,Q分别从点A,O同时出发,当点P运动到点B时,点Q随之停止运动,设运动时间为t(秒).
+10.一动点P从点A出发,在线段AB上以每秒2个单位长度的速度向点B运动;动点Q从点O出发在线段OC上以每秒1个单位长度的速度向点C运动,点P,Q分别从点A,O同时出发,当点P运动到点B时,点Q随之停止运动,设运动时间为t(秒).
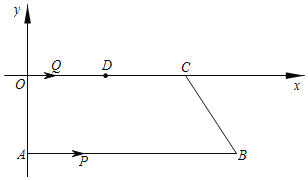
(1)求B,C两点的坐标;
(2)当t为何值时,四边形PQCB是平行四边形?
(3)点D为线段OC的中点,当t为何值时,△OPD是等腰三角形?直接写出t的所有值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B分别在函数y=![]() (k1>0)与函数y=
(k1>0)与函数y=![]() (k2<0)的图象上,线段AB的中点M在x轴上,△AOB的面积为4,则k1﹣k2的值为( )
(k2<0)的图象上,线段AB的中点M在x轴上,△AOB的面积为4,则k1﹣k2的值为( )

A.2B.4C.6D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应“双十二购物狂欢节”活动,某零食店推出了甲、乙、丙三类饼干礼包,已知甲、乙、丙三类礼包均由![]() 、
、![]() 、
、![]() 三种饼干搭配而成,每袋礼包的成本均为
三种饼干搭配而成,每袋礼包的成本均为![]() 、
、![]() 、
、![]() 三种饼干成本之和.每袋甲类礼包有5包
三种饼干成本之和.每袋甲类礼包有5包![]() 种饼干、2包
种饼干、2包![]() 种饼干、8包
种饼干、8包![]() 种饼干;每袋丙类礼包有7包
种饼干;每袋丙类礼包有7包![]() 种饼干、1包
种饼干、1包![]() 种饼干、4包
种饼干、4包![]() 种饼干.已知甲每袋成本是该袋中
种饼干.已知甲每袋成本是该袋中![]() 种饼干成本的3倍,利润率为
种饼干成本的3倍,利润率为![]() ,每袋乙的成本是其售价的
,每袋乙的成本是其售价的![]() ,利润是每袋甲利润的
,利润是每袋甲利润的![]() ;每袋丙礼包利润率为
;每袋丙礼包利润率为![]() .若该网店12月12日当天销售甲、乙、丙三种礼包袋数之比为
.若该网店12月12日当天销售甲、乙、丙三种礼包袋数之比为![]() ,则当天该网店销售总利润率为__________.
,则当天该网店销售总利润率为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)中x与y的部分对应值如表:
x | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
①ac<0;
②当x>1时,y的值随x值的增大而减小;
③x=3是方程ax2+(b﹣1)x+c=0的一个根;
④当﹣1<x<3时,ax2+(b﹣1)x+c>0.
上述结论中正确的个数是( )
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点O为对角线AC的中点,过点o作射线OG、ON分别交AB,BC于点E,F,且∠EOF=90°,BO、EF交于点P.则下列结论中:
⑴图形中全等的三角形只有两对;
⑵正方形ABCD的面积等于四边形OEBF面积的4倍;
⑶BE+BF= ![]() OA;
OA;
⑷AE2+CF2=2OPOB.
正确的结论有( )个.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知⊙A经过点E,B,C,O,且C(0,6)、E(﹣8,0)、O(0,0),则cos∠OBC的值为( )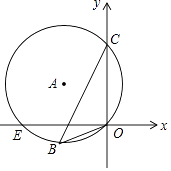
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com