
����Ŀ��Ϊ��Ӧ��˫ʮ������������ij��ʳ���Ƴ��˼ס��ҡ�����������������֪�ס��ҡ��������������![]() ��
��![]() ��
��![]() ���ֱ��ɴ�����ɣ�ÿ������ijɱ���Ϊ
���ֱ��ɴ�����ɣ�ÿ������ijɱ���Ϊ![]() ��
��![]() ��
��![]() ���ֱ��ɳɱ�֮��.ÿ�����������5��
���ֱ��ɳɱ�֮��.ÿ�����������5��![]() �ֱ��ɡ�2��
�ֱ��ɡ�2��![]() �ֱ��ɡ�8��
�ֱ��ɡ�8��![]() �ֱ��ɣ�ÿ�����������7��
�ֱ��ɣ�ÿ�����������7��![]() �ֱ��ɡ�1��
�ֱ��ɡ�1��![]() �ֱ��ɡ�4��
�ֱ��ɡ�4��![]() �ֱ���.��֪��ÿ���ɱ��Ǹô���
�ֱ���.��֪��ÿ���ɱ��Ǹô���![]() �ֱ��ɳɱ���3����������Ϊ
�ֱ��ɳɱ���3����������Ϊ![]() ��ÿ���ҵijɱ������ۼ۵�
��ÿ���ҵijɱ������ۼ۵�![]() ��������ÿ���������
��������ÿ���������![]() ��ÿ�������������Ϊ
��ÿ�������������Ϊ![]() .��������12��12�յ������ۼס��ҡ��������������֮��Ϊ
.��������12��12�յ������ۼס��ҡ��������������֮��Ϊ![]() �����������������������Ϊ__________.
�����������������������Ϊ__________.
���𰸡�25%
��������
��ÿ��A��B��C���ֱ��ɵijɱ��ֱ�Ϊx��y��z���Ӽ�������֣������5x=y+4z�����ɼ������������������ۼ�Ϊ19.5x���ɱ�15x������������ṩ�������������������ۼ�Ϊ12x���ɱ�Ϊ10x���ɱ�����������г�������ijɱ�Ϊ7x+y+4z=12x������ȷ����������ۼ�Ϊ15x���ɱ�Ϊ12x��������������ʵ�������������ʼ��ɣ�
�⣺��ÿ��A��B��C���ֱ��ɵijɱ��ֱ�Ϊx��y��z��������ã�
5x+2y+8z=15x��
��5x=y+4z��
�ɼ������������Ϊ30%��������������ۼ�Ϊ19.5x���ɱ�15x��
��ÿ���ҵijɱ������ۼ۵�![]() ��������ÿ��������
��������ÿ��������![]() ��
��
��֪ÿ��������������ǣ�4.5x��![]() =2x��
=2x��
����������ۼ�Ϊ12x���ɱ�Ϊ10x��
�ɱ��������ɿ�֪��������ijɱ�Ϊ��7x+y+4z=12x��
��ÿ�������������Ϊ��25%��
���������ۼ�Ϊ15x���ɱ�Ϊ12x��
�ס��ҡ��������������֮��Ϊ4��6��5��
��![]() ��
��
������������25%��
�ʴ�Ϊ��25%��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���ABC���������λ����ͼ(ÿ��С�����εı߳���Ϊ1)��
(1)�뻭����ABC��![]() ������ƽ��3����λ���ȣ�����
������ƽ��3����λ���ȣ�����![]() ������ƽ��2����λ���Ⱥ��
������ƽ��2����λ���Ⱥ��![]() (����
(����![]() �ֱ���A��B��C�Ķ�Ӧ�㣬��д����)��
�ֱ���A��B��C�Ķ�Ӧ�㣬��д����)��
(2)ֱ��д��![]() ��������ꣻ
��������ꣻ
(3)���ABC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У���E�ڱ�CD�ϣ����þ�����AE�۵���ʹ��D���ڱ�BC�ϵĵ�F��������F��FG��CD����AE�ڵ�G������DG��

��1����֤���ı���DEFGΪ���Σ�
��2����CD=8��CF=4����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������һ��������m�����m=k��k+1��������k�������������mΪ����������k Ϊm����Ѳ�ֵ㣮���磬56=7����7+1������56��һ������������7Ϊ56����Ѳ�ֵ㣮
��1����֤������������m��3�ı�������mһ����6�ı�����
��2���ѡ�������p�롰������q�IJ��Ϊ D��p��q��������p��q��D��p��q����0�����磬20=4��5��6=2��3���� D��20��6��=20��6=14������������p����Ѳ�ֵ�Ϊt����������q����Ѳ�ֵ�Ϊs���� D��p��q��=30ʱ���� ![]() �����ֵ��
�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ó��˾��![]() ��
��![]() �����ͺŵ���Ʒ���˳�����������Ʒ������������ֱ����±���ʾ��
�����ͺŵ���Ʒ���˳�����������Ʒ������������ֱ����±���ʾ��
�����������/���� | ��������/���� | |
| 0��8 | 0��5 |
| 2 | 1 |
��1����֪һ����Ʒ��![]() ��
��![]() �����ͺţ����һ����20�����ף�����һ����10��5�֣���
�����ͺţ����һ����20�����ף�����һ����10��5�֣���![]() ��
��![]() �����ͺ���Ʒ���м�����
�����ͺ���Ʒ���м�����
��2�����ʹ�˾���пɹ�ʹ�õĻ���ÿ�������3��5�֣��ݻ�Ϊ6�����ף����շѷ�ʽ���������֣�
�������շѣ�ÿ����������ﵽĿ�ĵ��շ�600Ԫ��
�ڰ����շѣ�ÿ�ֻ������䵽Ŀ�ĵ��շ�200Ԫ��
��Ҫ����1������Ʒһ�λ�������䵽Ŀ�ĵأ���������շѷ�ʽ�ɻ��ʹ�ã���ó��˾Ӧ���ѡ�����͡����ѷ�ʽ��ʹ�������˷����٣������˷��Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC���Ϊ1����һ�β������ֱ��ӳ�AB��BC��CA����A1��B1��C1��ʹA1B��AB��B1C��BC��C1A��CA��˳������A1��B1��C1���õ���A1B1C1���ڶ��β������ֱ��ӳ�A1B1��B1C1��C1A1����A2��B2��C2��ʹA2B1��A1B1��B2C1��B1C1��C2A1��C1A1��˳������A2��B2��C2���õ���A2B2C2�������˹��ɣ�Ҫʹ�õ��������ε��������2019�����پ������������β�����
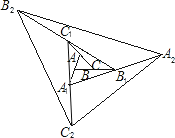
A.4B.5C.6D.7
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����һ����λ��Ȼ������������������λ�ϣ��ұ���λ�ϵ����ܱ������λ�ϵ�����1�������dz���������Ȼ���С������������磺123��3456��67�������ǡ���������
��1����ij����λ��������ǡ�õ������λ��76���������������Ϊ�� ����
��2��֤��������һ����λ����������ȥ����һ����λ��������֮���ټ�ȥ1�õ��Ľ�����ܱ�11������
��3�����һ����λ��Ȼ������������������λ�ϣ������λ�ϵ����ܱ��ұ���λ�ϵ�����1�������dz���������Ȼ���С���������������һ��ʮλΪ![]()
![]() Ϊ����������λ��������������һ����λΪ
Ϊ����������λ��������������һ����λΪ![]() Ϊ����������λ��������֮��Ϊ55�������λ��
Ϊ����������λ��������֮��Ϊ55�������λ��![]() Ϊ�������������������������������Ϊ
Ϊ�������������������������������Ϊ![]() ������
������![]() �����ֵ��
�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������50ǧ�ף�����������8��00С��ͬѧ�ڸ�����ͬ����ɽ�س��Ӽ�ǰ���ҵأ�2Сʱ��С���ĸ�����Ħ�г���ͬһ·��Ҳ�Ӽ�ǰ���ҵأ�������ʻ��·��y��ǧ�ף���С����ʻ��ʱ��x��Сʱ��֮��ĺ�����ϵ��ͼ��ʾ��С�����׳���Сʱʱ���н��е��������8ǧ�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��2��m���ǵ�һ������һ�㣬����OA����OA�Ƶ�A��ʱ����ת90��õ��߶�AB��������������y= ![]() ��x��0����ͼ��ǡ��ͬʱ������A��B����k��ֵΪ ��
��x��0����ͼ��ǡ��ͬʱ������A��B����k��ֵΪ �� 
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com