
【题目】对任意一个正整数m,如果m=k(k+1),其中k是正整数,则称m为“矩数”,k 为m的最佳拆分点.例如,56=7×(7+1),则56是一个“矩数”,7为56的最佳拆分点.
(1)求证:若“矩数”m是3的倍数,则m一定是6的倍数;
(2)把“矩数”p与“矩数”q的差记为 D(p,q),其中p>q,D(p,q)>0.例如,20=4×5,6=2×3,则 D(20,6)=20﹣6=14.若“矩数”p的最佳拆分点为t,“矩数”q的最佳拆分点为s,当 D(p,q)=30时,求 ![]() 的最大值.
的最大值.
【答案】
(1)证明:若“矩数”m=k(k+1)是3的倍数,则k(k+1)是3的倍数,k是正整数,
当k为奇数时,k+1是偶数,则k(k+1)是能被3整除的偶数,故k(k+1)是6的倍数;
当k为偶数时,则k(k+1)是能被3整除的偶数,故k(k+1)是6的倍数,
综上所述,若“矩数”m是3的倍数,则m一定是6的倍数
(2)解:根据题意得p=t(t+1),q=s(s+1),D(p,q)=t(t+1)﹣s(s+1)=30,
即t2+t﹣s2﹣s=30,
∴(t﹣s)(t+s+1)=30,
∵t,s是正整数,t>s,
∴t﹣s,t+s+1是正整数,且t+s+1>t﹣s,
∵30=1×30=2×15=3×10=5×6,
∴ ![]() 或
或 ![]() 或
或 ![]() 或
或 ![]() ,
,
解得: ![]() 或
或 ![]() 或
或 ![]() 或
或 ![]() ,
,
∵t,s是正整数,
∴符合条件的是: ![]() 或
或 ![]() 或
或 ![]() ,
,
∴ ![]() 或
或 ![]() =
= ![]() 或
或 ![]() =
= ![]() ,
,
∵ ![]() ,
,
∴ ![]() 的最大值是
的最大值是 ![]()
【解析】(1)连续的两个整数必是一奇数,一偶数,可分类证明;(2)可把新定义的规则转化为已知的规则,用已知代数式表示新运算法则,根据30的因数分解规则,求出最大值.
【考点精析】解答此题的关键在于理解因式分解的应用的相关知识,掌握因式分解是整式乘法的逆向变形,可以应用与数字计算、求值、整除性问题、判断三角形的形状、解方程.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:初中数学 来源: 题型:
【题目】二次函数 ![]() ,自变量x与函数y的对应值如下表:
,自变量x与函数y的对应值如下表:
x | … | -5 | -4 | -3 | -2 | -1 | 0 | … |
y | … | 4 | 0 | -2 | -2 | 0 | 4 | … |
下列说法正确的是( )
A.抛物线的开口向下
B.当x>-3时,y随x的增大而增大
C.二次函数的最小值是-2
D.抛物线的对称轴x= ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】位于南岸区黄桷垭的文峰塔,有着“平安宝塔”之称.某校数学社团对其高度 AB进行了测量.如图,他们从塔底A的点B出发,沿水平方向行走了13米,到达点C,然后沿斜坡CD继续前进到达点D处,已知DC=BC.在点D处用测角仪测得塔顶A的仰角为42°(点A,B,C,D,E在同一平面内).其中测角仪及其支架DE高度约为0.5米,斜坡CD的坡度(或坡比)i=1:2.4,那么文峰塔的高度AB约为( )(sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)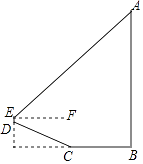
A.22.5 米
B.24.0 米
C.28.0 米
D.33.3 米
查看答案和解析>>
科目:初中数学 来源: 题型:
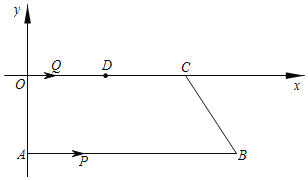
【题目】如图,在平面直角坐标系中,AB∥OC,A(0,﹣4),B(a,b),C(c,0),并且a,c满足c=![]() +10.一动点P从点A出发,在线段AB上以每秒2个单位长度的速度向点B运动;动点Q从点O出发在线段OC上以每秒1个单位长度的速度向点C运动,点P,Q分别从点A,O同时出发,当点P运动到点B时,点Q随之停止运动,设运动时间为t(秒).
+10.一动点P从点A出发,在线段AB上以每秒2个单位长度的速度向点B运动;动点Q从点O出发在线段OC上以每秒1个单位长度的速度向点C运动,点P,Q分别从点A,O同时出发,当点P运动到点B时,点Q随之停止运动,设运动时间为t(秒).
(1)求B,C两点的坐标;
(2)当t为何值时,四边形PQCB是平行四边形?
(3)点D为线段OC的中点,当t为何值时,△OPD是等腰三角形?直接写出t的所有值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从﹣4,﹣3,﹣2,﹣1,0,1,3,4,5这九个数中,随机抽取一个数,记为a,则数a使关于x的不等式组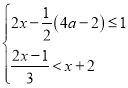 至少有四个整数解,且关于x的分式方程
至少有四个整数解,且关于x的分式方程![]() =1有非负整数解的概率是( )
=1有非负整数解的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应“双十二购物狂欢节”活动,某零食店推出了甲、乙、丙三类饼干礼包,已知甲、乙、丙三类礼包均由![]() 、
、![]() 、
、![]() 三种饼干搭配而成,每袋礼包的成本均为
三种饼干搭配而成,每袋礼包的成本均为![]() 、
、![]() 、
、![]() 三种饼干成本之和.每袋甲类礼包有5包
三种饼干成本之和.每袋甲类礼包有5包![]() 种饼干、2包
种饼干、2包![]() 种饼干、8包
种饼干、8包![]() 种饼干;每袋丙类礼包有7包
种饼干;每袋丙类礼包有7包![]() 种饼干、1包
种饼干、1包![]() 种饼干、4包
种饼干、4包![]() 种饼干.已知甲每袋成本是该袋中
种饼干.已知甲每袋成本是该袋中![]() 种饼干成本的3倍,利润率为
种饼干成本的3倍,利润率为![]() ,每袋乙的成本是其售价的
,每袋乙的成本是其售价的![]() ,利润是每袋甲利润的
,利润是每袋甲利润的![]() ;每袋丙礼包利润率为
;每袋丙礼包利润率为![]() .若该网店12月12日当天销售甲、乙、丙三种礼包袋数之比为
.若该网店12月12日当天销售甲、乙、丙三种礼包袋数之比为![]() ,则当天该网店销售总利润率为__________.
,则当天该网店销售总利润率为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,点M为BA延长线上一点,∠ABC的平分线BE和∠CAM的平分线AD相交于点P,分别交AC和BC的延长线于E,D.过P作PF⊥AD交AC的延长线于点H,交BC的延长线于点F,连接AF交DH于点G,则下列结论:①∠APB=45°;②PF=PA;③DG=AP+GH;④BD﹣AH=AB.其中正确的是_____(填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个长5m的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为4m,如果梯子的顶端A沿墙下滑1m至C点.
(1)求梯子底端B外移距离BD的长度;
(2)猜想CE与BE的大小关系,并证明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com