
【题目】如图,在平面直角坐标系中,点A(2,m)是第一象限内一点,连接OA,将OA绕点A逆时针旋转90°得到线段AB,若反比例函数y= ![]() (x>0)的图象恰好同时经过点A、B,则k的值为 .
(x>0)的图象恰好同时经过点A、B,则k的值为 . 
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】为响应“双十二购物狂欢节”活动,某零食店推出了甲、乙、丙三类饼干礼包,已知甲、乙、丙三类礼包均由![]() 、
、![]() 、
、![]() 三种饼干搭配而成,每袋礼包的成本均为
三种饼干搭配而成,每袋礼包的成本均为![]() 、
、![]() 、
、![]() 三种饼干成本之和.每袋甲类礼包有5包
三种饼干成本之和.每袋甲类礼包有5包![]() 种饼干、2包
种饼干、2包![]() 种饼干、8包
种饼干、8包![]() 种饼干;每袋丙类礼包有7包
种饼干;每袋丙类礼包有7包![]() 种饼干、1包
种饼干、1包![]() 种饼干、4包
种饼干、4包![]() 种饼干.已知甲每袋成本是该袋中
种饼干.已知甲每袋成本是该袋中![]() 种饼干成本的3倍,利润率为
种饼干成本的3倍,利润率为![]() ,每袋乙的成本是其售价的
,每袋乙的成本是其售价的![]() ,利润是每袋甲利润的
,利润是每袋甲利润的![]() ;每袋丙礼包利润率为
;每袋丙礼包利润率为![]() .若该网店12月12日当天销售甲、乙、丙三种礼包袋数之比为
.若该网店12月12日当天销售甲、乙、丙三种礼包袋数之比为![]() ,则当天该网店销售总利润率为__________.
,则当天该网店销售总利润率为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲船匀速顺流而下从![]() 港到
港到![]() 港,同时乙船匀速逆流而上从
港,同时乙船匀速逆流而上从![]() 港到
港到![]() 港,
港,![]() 港处于
港处于![]() 、
、![]() 两港的正中间,某个时刻,甲船接到通知需立即掉头逆流而上到
两港的正中间,某个时刻,甲船接到通知需立即掉头逆流而上到![]() 处,到
处,到![]() 处后迅速按原顺流速度驶向
处后迅速按原顺流速度驶向![]() 港,最后甲、乙两船都到达了各自的目的地.甲、乙两船在静水中的速度相同,设甲、乙两船与
港,最后甲、乙两船都到达了各自的目的地.甲、乙两船在静水中的速度相同,设甲、乙两船与![]() 港的距离之和为
港的距离之和为![]() ,行驶时间为
,行驶时间为![]() ,
,![]() 与
与![]() 的部分关系如图,则当两船在
的部分关系如图,则当两船在![]() 、
、![]() 间某处相超时,两船距离
间某处相超时,两船距离![]() 港的距离为________千米.
港的距离为________千米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个长5m的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为4m,如果梯子的顶端A沿墙下滑1m至C点.
(1)求梯子底端B外移距离BD的长度;
(2)猜想CE与BE的大小关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知⊙A经过点E,B,C,O,且C(0,6)、E(﹣8,0)、O(0,0),则cos∠OBC的值为( )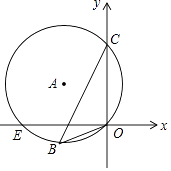
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明去文具店买文具,他与售货员的对话如下:
小明:你好.我要购买5支黑色水笔和3本笔记本.
售货员:好的.那你应该付34元.
小明:我把两种文具的单价弄反了,以为要付46元.
(1)求小明所购买的黑色水笔和笔记本的单价;
(2)如果小红也去购买同样的黑色水笔和笔记本,预算费用不超过88元,并且购买笔记本的数量要比购买黑色水笔的数量多1,那么小红最多能购买多少本笔记本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做“湘一四边形”.
(1)已知:如图1,四边形![]() 是“湘一四边形”,
是“湘一四边形”,![]() ,
,![]() ,
,![]() .则
.则![]() ,
, ![]() ,若
,若![]() ,
,![]() ,则
,则![]() (直接写答案)
(直接写答案)
(2)已知:在“湘一四边形”![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .求对角线
.求对角线![]() 的长(请画图求解),
的长(请画图求解),
(3)如图(2)所示,在四边形![]() 中,若
中,若![]() ,当
,当![]() 时,此时四边形
时,此时四边形![]() 是否是“湘一四边形”,若是,请说明理由:若不是,请进一步判断它的形状,并给出证明.
是否是“湘一四边形”,若是,请说明理由:若不是,请进一步判断它的形状,并给出证明.
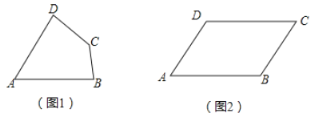
查看答案和解析>>
科目:初中数学 来源: 题型:
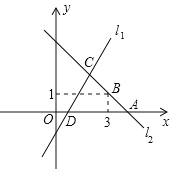
【题目】如图,直线l1的函数解析式为y=2x–2,直线l1与x轴交于点D.直线l2:y=kx+b与x轴交于点A,且经过点B(3,1),如图所示.直线l1、l2交于点C(m,2).
(1)求点D、点C的坐标;
(2)求直线l2的函数解析式;
(3)利用函数图象写出关于x、y的二元一次方程组![]() 的解.
的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB,∠CAB=40°,连接BD,OD,则∠AOD+∠ABD的度数为( )
A.100°
B.110°
C.120°
D.150°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com