Question

【题目】如图，直线l1的函数解析式为y=2x–2，直线l1与x轴交于点D．直线l2：y=kx+b与x轴交于点A，且经过点B（3，1），如图所示．直线l1、l2交于点C（m，2）．

（1）求点D、点C的坐标；

（2）求直线l2的函数解析式；

（3）利用函数图象写出关于x、y的二元一次方程组的解．

Answer 1

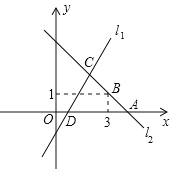
【答案】（1）D（1，0），C（2，2）；（2）y=–x+4；（3）．

【解析】

（1）求函数值为0时一次函数y=2x-2所对应的自变量的值即可得到D点横坐标，把C（m，2）代入y=2x-2求出m得到C点坐标；
（2）把C、B坐标代入y=kx+b中，利用待定系数法求直线l2的解析式；
（3）利用方程组的解就是两个相应的一次函数图象的交点坐标求解．

（1）∵点D为直线l1：y=2x–2与x轴的交点，

∴当y=0时，0=2x–2，解得x=1，

∴D（1，0）；

∵点C在直线l1：y=2x–2上，

∴2=2m–2，解得m=2，

∴点C的坐标为（2，2）；

（2）∵点C（2，2）、B（3，1）在直线l2上，

∴，

解得，

∴直线l2的解析式为y=–x+4；

（3）由图可知二元一次方程组的解为．