
【题目】如图,正方形![]() 的边长为2,
的边长为2,![]() 为坐标原点,
为坐标原点,![]() 和
和![]() 分别在
分别在![]() 轴、
轴、![]() 轴上,点
轴上,点![]() 是
是![]() 边的中点,过点
边的中点,过点![]() 的直线
的直线![]() 交线段
交线段![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() 平分
平分![]() ,则
,则![]() 的值为__________.
的值为__________.

【答案】1或3
【解析】
分两种情况:①当点F在DC之间时,作出辅助线,求出点F的坐标即可求出k的值;②当点F与点C重合时求出点F的坐标即可求出k的值.
解:①如图,作AG⊥EF交EF于点G,连接AE,

∵AF平分∠DFE,
∴DA=AG=2,
在Rt△ADF和Rt△AGF中,![]()
∴Rt△ADF≌Rt△AGF(HL)
∴DF=FG,
∴点E是BC边的中点,
∴BE=CE=1,
∵在Rt△FCE中,EF2=FC2+CE2,
即(DF+1)2=(2-DF)2+1,
解得:DF=![]() ,
,
∴点F (![]() ,2)
,2)
把点F的坐标代入![]() 得:2=
得:2=![]() k,解得k=3
k,解得k=3
②当点F与点C重合时,
∵四边形ABCD是正方形,∴AF平分∠DFE
∴F(2,2)
把点F的坐标代入![]() 得:2=2k,解得k=1
得:2=2k,解得k=1
故答案为:1或3


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
【题目】如图,一个长5m的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为4m,如果梯子的顶端A沿墙下滑1m至C点.
(1)求梯子底端B外移距离BD的长度;
(2)猜想CE与BE的大小关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
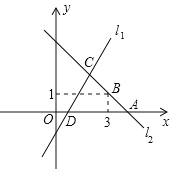
【题目】如图,直线l1的函数解析式为y=2x–2,直线l1与x轴交于点D.直线l2:y=kx+b与x轴交于点A,且经过点B(3,1),如图所示.直线l1、l2交于点C(m,2).
(1)求点D、点C的坐标;
(2)求直线l2的函数解析式;
(3)利用函数图象写出关于x、y的二元一次方程组![]() 的解.
的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知OM⊥ON,垂足为O,点A、B分别是射线OM、ON上的一点(O点除外).

(1)如图①,射线AC平分∠OAB,若BC所在的直线也平分以B为顶点的某一个角α(0°<α<180°),则∠ACB= ;
(2)如图②,P为平面上一点(O点除外),∠APB=90°,且OA≠AP,分别画∠OAP、∠OBP的平分线AD、BE,交BP、OA于点D、E,试判断AD与BE的位置关系,并说明理由;
(3)在(2)的条件下,随着P点在平面内运动,AD、BE的位置关系是否发生变化?请利用图③画图探究.如果不变,直接回答;如果变化,画出图形,写出AD、BE位置关系并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市荸荠喜获丰收,某生产基地收获荸荠40吨.经市场调查,可采用批发、零售、加工销售三种销售方式,这三种销售方式每吨荸荠的利润如下表:
销售方式 批发 零售 加工销售
利润(百元/吨) 12 22 30
设按计划全部售出后的总利润为y百元,其中批发量为x吨,且加工销售量为15吨.
(1)求y与x之间的函数关系式;
(2)若零售量不超过批发量的4倍,求该生产基地按计划全部售完荸荠后获得的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从![]() 地出发向
地出发向![]() 地行走,同时晓阳从
地行走,同时晓阳从![]() 地出发向
地出发向![]() 地行走,如图所示,相交于点
地行走,如图所示,相交于点![]() 的两条线段
的两条线段![]() 、
、![]() 分别表示小明、晓阳离
分别表示小明、晓阳离![]() 地的距离
地的距离![]() (千米)与已用时间
(千米)与已用时间![]() (分钟)之间的关系.
(分钟)之间的关系.
(1)小明与晓阳相遇时,晓阳出发的时间是__________;
(2)求晓阳到达![]() 地的时间.
地的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB,∠CAB=40°,连接BD,OD,则∠AOD+∠ABD的度数为( )
A.100°
B.110°
C.120°
D.150°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现:如图 1,已知点 F,G 分别在直线 AB,CD 上,且 AB∥CD,若∠BFE=40°,∠CGE=130°,则∠GEF 的度数为 ;

(2)拓展探究:∠GEF,∠BFE,∠CGE 之间有怎样的数量关系?写出结论并给出证明; 答:∠GEF= .
证明:过点 E 作 EH∥AB,

∴∠FEH=∠BFE( ),
∵AB∥CD,EH∥AB,(辅助线的作法)
∴EH∥CD( ),
∴∠HEG=180°-∠CGE( ),
∴∠FEG=∠HFG+∠FEH= .
(3)深入探究:如图 2,∠BFE 的平分线 FQ 所在直线与∠CGE 的平分线相交于点 P,试探究∠GPQ 与∠GEF 之间的数量关系,请直接写出你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com