Question

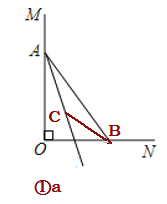
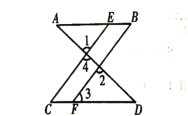
【题目】如图，已知OM⊥ON，垂足为O，点A、B分别是射线OM、ON上的一点（O点除外）．

（1）如图①，射线AC平分∠OAB，若BC所在的直线也平分以B为顶点的某一个角α（0°＜α＜180°），则∠ACB＝　 ；

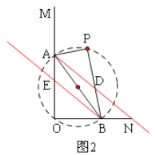
（2）如图②，P为平面上一点（O点除外），∠APB＝90°，且OA≠AP，分别画∠OAP、∠OBP的平分线AD、BE，交BP、OA于点D、E，试判断AD与BE的位置关系，并说明理由；

（3）在（2）的条件下，随着P点在平面内运动，AD、BE的位置关系是否发生变化？请利用图③画图探究．如果不变，直接回答；如果变化，画出图形，写出AD、BE位置关系并说明理由．

Answer 1

【答案】（1）45°或135°；（2）AD∥BE，理由见解析；（3）变化；当P在AB的上方时，如图②见解析，有AD∥BE； 当P在AB的下方时，如图③见解析，有AD⊥BE．理由见解析．

【解析】

（1）分两种情况讨论：若BC平分∠ABO，由三角形内角和定理可得结论，若BC平分∠ABO的外角，根据三角形外角的性质和角平分线的定义，可得结论；

（2）证明∠OAD=∠OEB，可得：AD∥BE；

（3）先根据∠AOB=∠APB=90°，分点P在AB的上方和P在AB的下方分类，依据角平分线的定义及特殊构图“8”字形对顶三角形有关角的关系的运用，即可得到结论．

（1）若BC平分∠ABO，如图①a，

∵∠AOB=90°，

∴∠OAB+∠ABO=90°，

∵AC，BC分别平分∠OAB，∠ABO，

∴∠BAC=∠OAB，∠ABC=∠ABO,

∴∠BAC+∠ABC=（∠OAB+∠ABO）=45°

∴∠ACB=180°-(∠BAC+∠ABC)= 180°-45°=135°

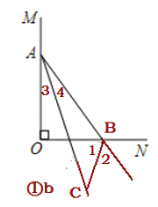
若BC平分∠ABO的外角，如图①b，

同上易知，∠1=∠2，∠3=∠4

∵∠1+∠2=∠3+∠4+∠AOB=∠3+∠4+90°，

∴2∠2=2∠4+90°，

∴∠2=∠4+45°，

∴∠2-∠4=45°，

∴∠ACB=45°，

综上，∠ACB=45°或135°.

故答案为：45°或135°.

（2）AD∥BE

∵∠AOB＝∠P＝90°

∴∠OAP+∠OBP＝180°

∴∠OAP+∠OBP＝90°

∵AD平分∠OAP，BE平分∠OBP

∴∠OAD＝∠OAP，∠OBE＝∠OBP

∴∠OAD+∠OBE=∠OAP+∠OBP＝90°

∵∠AOB＝90°

∴∠OEB+∠OBE＝90°

∴∠OAD＝∠OEB

∴AD∥BE

（3）变化

当P在AB的上方时，如图②，有AD∥BE；

当P在AB的下方时，如图③，有AD⊥BE

理由是：

延长AD与BE交于点G,设OA与PB交于H，

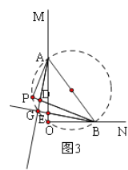
∵∠APB＝∠AOB＝90°，∠AHP＝∠BHO

∴∠OAP＝∠OBP

∵AD平分∠OAP，BE平分∠OBP

∴∠PAD＝∠OAP，∠DBE＝∠OBP

∴∠PAD＝∠DBE，

又∵∠ADP＝∠BDG，

∴∠AGB＝∠P＝90°，

∴AD⊥BE．