
【题目】如图,平行四边形![]() 中,对角线
中,对角线![]() 、
、![]() 相交于
相交于![]() ,
,![]() ,
,![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 的中点,下列结论:①
的中点,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 平分
平分![]() ;⑤四边形
;⑤四边形![]() 是菱形,其中正确的个数是( )
是菱形,其中正确的个数是( )

A.5B.4C.3D.2
【答案】C
【解析】
根据平行四边形的性质可得OB=BC,由等腰三角形的性质可判断①正确,由直角三角形的性质和三角形中位线定理可判断②错误,通过证四边形BGFE是平行四边形,可判断③正确,由平行线的性质和等腰三角形的性质可判断④正确,假设结论成立得到∠BAC=30°,与题意不符合,即可判断⑤错误.
解: ∵四边形ABCD是平行四边形.
∴.BO=DO=![]() BD,AD=BC,AB=CD,AB∥DC,
BD,AD=BC,AB=CD,AB∥DC,
又∵BD=2AD,
∴OB= BC=OD=DA,∴△OBC是等腰三角形,且点E是OC中点,
∴BE⊥AC,
故①正确;
∵E、F分别是OC、OD的中点,
∴EF //CD,EF=![]() CD,
CD,
∵点G是Rt△ABE斜边AB上的中点,
∴GE=![]() AB=AG= BG
AB=AG= BG
∴EG=EF=AG=BG,无法证明GE=GF,
假设GE=GF成立,即GE=GF=BG=AG成立,则∠ABE=60°∴∠BAC=30°这不符合题意,
故②错误;
∵BG=EF, EF∥CD∥AB,
∴四边形BGFE是平行四边形,
∴GE=BE,且BG=EF,GE=GE,
∴△BGE≌△FEG(SSS)
故③正确;
∵EF∥CD∥AB,
∴∠BAC=∠ACD=∠AEF
∵AG=GE
∴∠GAE=∠AEG,
∴∠AEG=∠AEF
∴AE平分∠GEF,
故④正确,
若四边形BEFG是菱形
∴BE=BG=![]() AB,
AB,
∴∠BAC= 30°
与题意不符合
故⑤错误,
故选: C.


科目:初中数学 来源: 题型:
【题目】阅读理解:
材料1:对于一个关于![]() 的二次三项式
的二次三项式![]() ,除了可以利用配方法求该多项式的取值范围外,爱思考的小川同学还想到了其他的方法;比如先令
,除了可以利用配方法求该多项式的取值范围外,爱思考的小川同学还想到了其他的方法;比如先令![]() ,然后移项可得:
,然后移项可得:![]() ,再利用一元二次方程根的判别式来确定
,再利用一元二次方程根的判别式来确定![]() 的取值范围,请仔细阅读下面的例子:
的取值范围,请仔细阅读下面的例子:
例:求![]() 的取值范围;
的取值范围;
解:令![]()
![]()
![]()
![]()
![]() ;
;
材料2:在学习完一元二次方程的解法后,爱思考的小川同学又想到仿造一元二次方程的解法来解决一元二次不等式的解集问题,他的具体做法如下:
若关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的实数根
有两个不相等的实数根![]() 、
、![]() ,则关于
,则关于![]() 的一元二次不等式
的一元二次不等式![]() 的解集为:
的解集为:![]() 或
或![]() ;则关于
;则关于![]() 的一元二次不等式的
的一元二次不等式的![]() 的解集为:
的解集为:![]() .
.
材料3:若关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的实数根
有两个不相等的实数根![]() 、
、![]() ;则
;则![]() ;
;![]() ,我们称之为韦达定理;
,我们称之为韦达定理;
请根据上述材料,解答下列问题:
(1)若关于![]() 的二次三项式
的二次三项式![]() (
(![]() 为常数)的最小值为
为常数)的最小值为![]() ,则
,则![]() ________.
________.
(2)求出代数式![]() 的取值范围.
的取值范围.
(3)若关于![]() 的代数式
的代数式![]() (其中
(其中![]() 、
、![]() 为常数,且
为常数,且![]() )的最小值为
)的最小值为![]() ,最大值为4,请求出满足条件的
,最大值为4,请求出满足条件的![]() 、
、![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
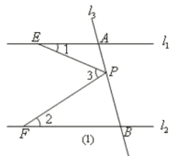
【题目】如图 ,已知直线l1,l2,点P在直线l3上且不与点A、B重合.记∠AEP=∠1,∠BFP=∠2,∠EPF=∠3.
(1) 如图 ,若直线l1//l2,点P在线段AB(A、B两点除外)上运动时,写出∠1、∠2、∠3之间的关系,并说明理由.
(2)如图 ,若(1)中∠1、∠2、∠3之间的关系成立,你能不能反向推出直线l1//l2?若成立请说明理由.
(3)如图 ,若直线l1//l2,若点P在A、B两点外侧运动时(不包括线段AB),请直接写出∠1、∠2、∠3之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小楠是一个乐学习,善思考,爱探究的同学,她对函数![]() 的图象和性质进行了探究,请你将下列探究过程补充完整:
的图象和性质进行了探究,请你将下列探究过程补充完整:
(Ⅰ)函数![]() 的自变量x的取值范围是 .
的自变量x的取值范围是 .
(Ⅱ)用描点法画函数图象:
(i)列表:
x | … | ﹣5 | ﹣2 | ﹣1 | 0 | … | 2 | 3 | 4 | 7 | … |
y | … | a | 2 | 3 | b | … | 6 | 3 | 2 | 1 | … |
表中a的值为 ,b的值为 .
(ii)描点连线:请在下图画出该图象的另一部分.

(Ⅲ)观察函数图象,得到函数![]() 的性质:
的性质:
当x 时,函数值y随x的增大而 ;
当x 时,函数值y随x的增大而减少.
(IV)应用:若![]() ≥6,则x的取值范围是 .
≥6,则x的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知OM⊥ON,垂足为O,点A、B分别是射线OM、ON上的一点(O点除外).

(1)如图①,射线AC平分∠OAB,若BC所在的直线也平分以B为顶点的某一个角α(0°<α<180°),则∠ACB= ;
(2)如图②,P为平面上一点(O点除外),∠APB=90°,且OA≠AP,分别画∠OAP、∠OBP的平分线AD、BE,交BP、OA于点D、E,试判断AD与BE的位置关系,并说明理由;
(3)在(2)的条件下,随着P点在平面内运动,AD、BE的位置关系是否发生变化?请利用图③画图探究.如果不变,直接回答;如果变化,画出图形,写出AD、BE位置关系并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,某市坚持绿色发展理念,着力建设生态典范城市,大力开展绿化工程建设.某校“社会实践”小组的同学为了了解该市绿地的发展情况,对市园林局进行了走访调查,获取了如下信息:
信息1:2015年的绿地总面积(绿地总面积=森林面积+草场面积)为276km2 , 其中森林面积比上一年增长40%,草地面积比上一年增长20%.
信息2:2014年的绿地总面积为200km2 . 
求:
(1)该市2014年的森林面积和草场面积分别为多少km2?
(2)若该市2016年的绿地总面积为338km2 , 求2014年至2016年该市绿地总面积的年平均增长率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从![]() 地出发向
地出发向![]() 地行走,同时晓阳从
地行走,同时晓阳从![]() 地出发向
地出发向![]() 地行走,如图所示,相交于点
地行走,如图所示,相交于点![]() 的两条线段
的两条线段![]() 、
、![]() 分别表示小明、晓阳离
分别表示小明、晓阳离![]() 地的距离
地的距离![]() (千米)与已用时间
(千米)与已用时间![]() (分钟)之间的关系.
(分钟)之间的关系.
(1)小明与晓阳相遇时,晓阳出发的时间是__________;
(2)求晓阳到达![]() 地的时间.
地的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由一些棱长为1的小立方块所搭几何体的三种视图.若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个长方体,至少还需要个小立方块.最终搭成的长方体的表面积是 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com