
【题目】如图,已知![]() 中,
中,![]() ,
,![]() ,D是AC的中点,E是BC延长线上的一点,且
,D是AC的中点,E是BC延长线上的一点,且![]() ,
,![]() ,垂足为M.
,垂足为M.

![]() 求
求![]() 的度数;
的度数;
![]() 求证:M是BE的中点.
求证:M是BE的中点.
【答案】![]() 30°;(2)见解析.
30°;(2)见解析.
【解析】
(1)先推出△ABC是等边△ABC,再根据等边三角形的性质得到∠ACB=∠ABC=60°,然后根据等边对等角可得:∠E=∠CDE,最后根据外角的性质可求∠E的度数;
(2)连接BD,由等边三角形的三线合一的性质可得:![]() ,结合(1)的结论可得:∠DBC=∠E,然后根据等角对等边,可得:DB=DE,最后根据等腰三角形的三线合一的性质可得:M是BE的中点.
,结合(1)的结论可得:∠DBC=∠E,然后根据等角对等边,可得:DB=DE,最后根据等腰三角形的三线合一的性质可得:M是BE的中点.
(1)解:∵![]() 中,
中,![]() ,
,![]()
∴三角形ABC是等边△ABC,
∴∠ACB=∠ABC=60°,
又∵CE=CD,
∴∠E=∠CDE,
又∵∠ACB=∠E+∠CDE,
∴![]() ;
;
(2)证明:连接BD,
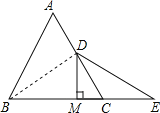
∵等边△ABC中,D是AC的中点,
∴![]()
由(1)知∠E=30°
∴∠DBC=∠E=30°
∴DB=DE
又∵DM⊥BC
∴M是BE的中点.


科目:初中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,
中,![]() 分别为边
分别为边![]() 的中点,
的中点,![]() 是对角线,过点
是对角线,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() .
.
(2)若![]() ,
,
①求证:四边形![]() 是菱形.
是菱形.
②当![]() 时,求四边形
时,求四边形![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形![]() 中,对角线
中,对角线![]() 、
、![]() 相交于
相交于![]() ,
,![]() ,
,![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 的中点,下列结论:①
的中点,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 平分
平分![]() ;⑤四边形
;⑤四边形![]() 是菱形,其中正确的个数是( )
是菱形,其中正确的个数是( )

A.5B.4C.3D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 是坐标原点,四边形
是坐标原点,四边形![]() 是菱形,点
是菱形,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴的负半轴上,直线
轴的负半轴上,直线![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() 边交
边交![]() 轴于点
轴于点![]() .
.
(1)如图1,求直线![]() 的解析式;
的解析式;

(2)如图2,连接![]() ,动点
,动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 方向以1个单位/秒的速度向终点
方向以1个单位/秒的速度向终点![]() 匀速运动,设
匀速运动,设![]() 的面积为
的面积为![]() (
(![]() ),点
),点![]() 的运动时间为
的运动时间为![]() 秒,求
秒,求![]() 与
与![]() 之间的函数关系式,并直接写出自变量
之间的函数关系式,并直接写出自变量![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() ,
,![]() 被直线
被直线![]() 所截,
所截,![]() ,
,![]() 是平面内任意一点(点
是平面内任意一点(点![]() 不在直线
不在直线![]() ,
,![]() ,
,![]() 上),设
上),设![]() ,
,![]() .下列各式:①
.下列各式:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,
,![]() 的度数可能是( )
的度数可能是( )

A.①②③B.①②④C.①③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】复杂的数学问题我们常会把它分解为基本问题来研究,化繁为简,化整为零这是一种常见的数学解题思想.
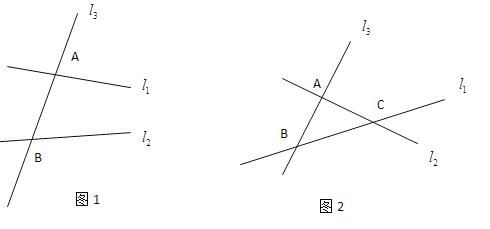
(1)如图1,直线![]() ,
,![]() 被直线
被直线![]() 所截,在这个基本图形中,形成了______对同旁内角.
所截,在这个基本图形中,形成了______对同旁内角.
(2)如图2,平面内三条直线![]() ,
,![]() ,
,![]() 两两相交,交点分别为
两两相交,交点分别为![]() 、
、![]() 、
、![]() ,图中一共有______对同旁内角.
,图中一共有______对同旁内角.
(3)平面内四条直线两两相交,最多可以形成______对同旁内角.
(4)平面内![]() 条直线两两相交,最多可以形成______对同旁内角.
条直线两两相交,最多可以形成______对同旁内角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】假山具有多方面的造景功能,与建筑、植物等组合成富于变化的景致.某公园有一座假山,小亮、小慧等同学想用一些测量工具和所学的几何知识测量这座假山的高度来检验自己掌握知识和运用知识的能力,如图,在阳光下,小亮站在水平地面的D处,此时小亮身高的影子顶端与假山的影子顶端E重合,这时小亮身高CD的影长DE=2米,一段时间后,小亮从D点沿BD的方向走了3.6米到达G处,此时小亮身高的影子顶端与假山的影子顶端H重合,这时小亮身高的影长GH=2.4米,已知小亮的身高CD=FG=1.5米,点G,E,D均在直线BH上,AB⊥BH,CD⊥BH,GF⊥BH,请你根据题中提供的相关信息,求出假山的高度AB.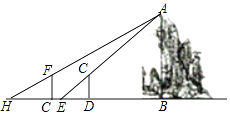
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了![]() (n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应
(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应![]() 展开式中的系数;第四行的四个数1,3,3,1,恰好对应着
展开式中的系数;第四行的四个数1,3,3,1,恰好对应着![]() 展开式中的系数等等.
展开式中的系数等等.

(1)根据上面的规律,写出![]() 的展开式.
的展开式.
(2)利用上面的规律计算:![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com