
【题目】小楠是一个乐学习,善思考,爱探究的同学,她对函数![]() 的图象和性质进行了探究,请你将下列探究过程补充完整:
的图象和性质进行了探究,请你将下列探究过程补充完整:
(Ⅰ)函数![]() 的自变量x的取值范围是 .
的自变量x的取值范围是 .
(Ⅱ)用描点法画函数图象:
(i)列表:
x | … | ﹣5 | ﹣2 | ﹣1 | 0 | … | 2 | 3 | 4 | 7 | … |
y | … | a | 2 | 3 | b | … | 6 | 3 | 2 | 1 | … |
表中a的值为 ,b的值为 .
(ii)描点连线:请在下图画出该图象的另一部分.

(Ⅲ)观察函数图象,得到函数![]() 的性质:
的性质:
当x 时,函数值y随x的增大而 ;
当x 时,函数值y随x的增大而减少.
(IV)应用:若![]() ≥6,则x的取值范围是 .
≥6,则x的取值范围是 .
【答案】(Ⅰ)x≠1;(Ⅱ)(i)1,6,(ii)作图见解析;(Ⅲ)<1,增大,>1;(Ⅳ)0≤x<1或1<x≤2.
【解析】
(Ⅰ)分母不为零,据此求解;
(Ⅱ)(i)把![]() =-5、0分别代入函数表达式,即可求解;
=-5、0分别代入函数表达式,即可求解;
(ii)用平滑的曲线连接即可画出函数图像;
(Ⅲ)观察函数图像,可得函数性质;
(Ⅳ)由函数图像,即可求得.
(Ⅰ)x﹣1≠0,解得x≠1,
故答案为x≠1;
(Ⅱ)(i)当x=﹣5时,a=y=![]() =1,b=y=
=1,b=y=![]() =6,
=6,
故答案为1,6;
(ii)描点后画出如下函数图象:
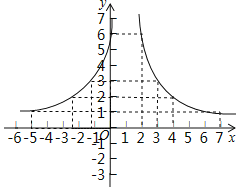
(Ⅲ)观察函数图象,得到函数![]() 的性质:
的性质:
当x<1时,函数值y随x的增大而增大;
当x>1时,函数值y随x的增大而减少.
故答案为<1,增大;>1;
(Ⅳ)由图象可知,![]() ≥6时x的取值范围是0≤x<1或1<x≤2,
≥6时x的取值范围是0≤x<1或1<x≤2,
故答案为:0≤x<1或1<x≤2.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=10,AD=16,∠A=60°,P是射线AD上一点,连接PB,沿PB将△APB折叠,得到△A′PB.
(1)如图2所示,当PA′⊥BC时,求线段PA的长度.
(2)当∠DPA′=10°时,求∠APB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,
中,![]() 分别为边
分别为边![]() 的中点,
的中点,![]() 是对角线,过点
是对角线,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() .
.
(2)若![]() ,
,
①求证:四边形![]() 是菱形.
是菱形.
②当![]() 时,求四边形
时,求四边形![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,LA,LB分别表示A步行与B骑车在同一路上行驶的路程y(千米)与时间x(小时)的关系.根据图象,回答下列问题:

(1)B出发时与A相距 千米.
(2)B骑车一段路后,自行车发生故障,进行修理,所用的时间是 小时.
(3)B出发后 小时与A相遇.
(4)求出A行走的路程y与时间x的函数关系式.(写出过程)
(5)若B的自行车不发生故障,保持出发时的速度匀速行驶,A,B肯定会提前相遇.在图中画出这种假设情况下B骑车行驶过程中路程y与时间x的函数图象,在图中标出这个相遇点P,并回答相遇点P离B的出发点O相距多少千米.(写出过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一种阳台户外伸缩晾衣架,侧面示意图如图2所示,其支架AB,CD,EF,GH,BE,DG,FK的长度都为40cm(支架的宽度忽略不计),四边形BQCP、DMEQ、FNGM是互相全等的菱形,当晾衣架的A端拉伸到距离墙壁最远时,∠B=∠D=∠F=80°,这时A端到墙壁的距离约为cm.
(sin40°≈0.643,cos40°≈0.766,tan40°≈0.839)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是直角三角形,∠ACB=90°,∠A=30°
(1)实践与操作:利用尺规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法).
①作△ABC的外接圆O;
②在AB的延长线上作一点D,使得CD与⊙O相切;
(2)综合与运用:在你所作的图中,若AC=6,则由线段CD,BD及 ![]() 所围成图形的面积为 .
所围成图形的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形![]() 中,对角线
中,对角线![]() 、
、![]() 相交于
相交于![]() ,
,![]() ,
,![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 的中点,下列结论:①
的中点,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 平分
平分![]() ;⑤四边形
;⑤四边形![]() 是菱形,其中正确的个数是( )
是菱形,其中正确的个数是( )

A.5B.4C.3D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 是坐标原点,四边形
是坐标原点,四边形![]() 是菱形,点
是菱形,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴的负半轴上,直线
轴的负半轴上,直线![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() 边交
边交![]() 轴于点
轴于点![]() .
.
(1)如图1,求直线![]() 的解析式;
的解析式;

(2)如图2,连接![]() ,动点
,动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 方向以1个单位/秒的速度向终点
方向以1个单位/秒的速度向终点![]() 匀速运动,设
匀速运动,设![]() 的面积为
的面积为![]() (
(![]() ),点
),点![]() 的运动时间为
的运动时间为![]() 秒,求
秒,求![]() 与
与![]() 之间的函数关系式,并直接写出自变量
之间的函数关系式,并直接写出自变量![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了![]() (n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应
(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应![]() 展开式中的系数;第四行的四个数1,3,3,1,恰好对应着
展开式中的系数;第四行的四个数1,3,3,1,恰好对应着![]() 展开式中的系数等等.
展开式中的系数等等.

(1)根据上面的规律,写出![]() 的展开式.
的展开式.
(2)利用上面的规律计算:![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com