
【题目】如图1是甲、乙两个圆柱形水槽的轴截面示意图.乙槽中有一圆柱形铁块放在其中(圆柱形铁块的下底面完全落在水槽底面上),现将甲槽中的水匀速注人乙槽.甲、乙两个水槽中水的深度![]() 与注水时间
与注水时间![]() (分钟)之间的关系如图2所示.根据图象提供的信息,解答下列问题:
(分钟)之间的关系如图2所示.根据图象提供的信息,解答下列问题:
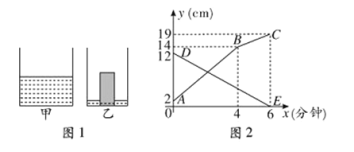
(1)图2中折线![]() 表示 槽中的水的深度与注水时间的关系,线段
表示 槽中的水的深度与注水时间的关系,线段![]() 表示 槽中的水的深度与注水时间的关系(填“甲”或“乙”),点
表示 槽中的水的深度与注水时间的关系(填“甲”或“乙”),点![]() 的纵坐标表示的实际意义是 ;
的纵坐标表示的实际意义是 ;
(2)当![]() 时,分别求出
时,分别求出![]() 和
和![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)注水多长时间时,甲、乙两个水槽中的水深度相同?
(4)若乙槽底面积为![]() 平方厘米(壁厚不计) ,求乙槽中铁块的体积.
平方厘米(壁厚不计) ,求乙槽中铁块的体积.
【答案】(1)乙;甲;乙槽中圆柱形铁块的高度是14厘米;(2)y甲=-2x+12,y乙=3x+2;(3)注水2分钟;(4)84cm3
【解析】
(1)根据题目中甲槽向乙槽注水可以得到折线ABC是乙槽中水的深度与注水时间之间的关系,点B表示的实际意义是乙槽内液面恰好与圆柱形铁块顶端相平;
(2)根据题意分别求出两个水槽中y与x的函数关系式即可;
(3)根据(2)中y与x的函数关系式,令y相等即可得到水位相等的时间;
(4)用水槽的体积减去水槽中水的体积即可得到铁块的体积;
解:(1)由题意可得:
∵乙槽中含有铁块,
∴乙槽中水深不是匀速增长,
∴折线![]() 表示乙槽中水深与注水时间的关系,
表示乙槽中水深与注水时间的关系,
线段DE表示甲槽中水深与注水时间的关系,
由点B的坐标可得:
点B的纵坐标表示的实际意义是:乙槽中圆柱形铁块的高度是14厘米;
故答案为:乙;甲;乙槽中圆柱形铁块的高度是14厘米;
(2)设线段AB、DE的解析式分别为:y甲=k1x+b1,y乙=k2x+b2,
∵AB经过点(0,2)和(4,14),DE经过(0,12)和(6,0),
∴ ,
,
解得:![]() ,
,
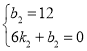 ,
,
解得: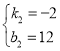 ,
,
∴当![]() 时, y甲=-2x+12,y乙=3x+2;
时, y甲=-2x+12,y乙=3x+2;
(3)由(2)可知:
令y甲=y乙,
即3x+2=-2x+12,
解得x=2,
∴当2分钟时两个水槽水面一样高.
(4)由图象知:当水槽中没有没过铁块时4分钟水面上升了12cm,即1分钟上升3cm,
当水面没过铁块时,2分钟上升了5cm,即1分钟上升2.5cm,
设铁块的底面积为acm2,
则乙水槽中不放铁块的体积为:2.5×36cm3,
放了铁块的体积为3×(36-a)cm3,
∴1×3×(36-a)=1×2.5×36,
解得a=6,
∴铁块的体积为:6×14=84(cm3).


科目:初中数学 来源: 题型:
【题目】某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核.甲、乙、丙各项得分如下表:
笔 试 | 面 试 | 体 能 | |
甲 | 85 | 80 | 75 |
乙 | 80 | 90 | 73 |
丙 | 83 | 79 | 90 |
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序.
(2)该公司规定:笔试,面试、体能得分分别不得低于80分,80分,70分,并按60%,30%,10%的比例计入总分(不计其他因素条件),请你说明谁将被录用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程或方程组解应用题:
为了响应“十三五”规划中提出的绿色环保的倡议,某校文印室提出了每个人都践行“双面打印,节约用纸”.已知打印一份资料,如果用A4厚型纸单面打印,总质量为400克,将其全部改成双面打印,用纸将减少一半;如果用A4薄型纸双面打印,这份资料的总质量为160克,已知每页薄型纸比厚型纸轻0.8克,求A4薄型纸每页的质量.(墨的质量忽略不计)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋中装有4个只有颜色不同的球,其中1个黄球、1个蓝球、2个红球.
(1)任意摸出1个球,记下颜色后不放回,再任意摸出1个球.求两次摸出的球恰好都是红球的概率(要求画树状图或列表);
(2)现再将n个黄球放入布袋,搅匀后,使任意摸出1个球是黄球的概率为![]() ,求n的值.
,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
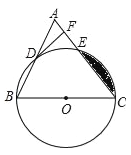
【题目】如图,已知在△ABC中,BC=AC,以BC为直径的⊙O与边AB、AC分别交于点D、E,DF⊥AC于点F.
(1)求证:点D是AB的中点;
(2)判断DF与⊙O的位置关系,并证明你的结论;
(3)若⊙O的半径为10,sinB=![]() ,求阴影部分面积.
,求阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(类比概念)三角形的内切圆是以三个内角的平分线的交点为圆心,以这点到三边的距离为半径的圆,则三角形可以称为圆的外切三角形,可以得出三角形的三边与该圆相切.以此类推,如图1,各边都和圆相切的四边形称为圆外切四边形
(性质探究)如图1,试探究圆外切四边形的ABCD两组对边AB,CD与BC,AD之间的数量关系
猜想结论: (要求用文字语言叙述)
写出证明过程(利用图1,写出已知、求证、证明)
(性质应用)
①初中学过的下列四边形中哪些是圆外切四边形 (填序号)
A:平行四边形:B:菱形:C:矩形;D:正方形
②如图2,圆外切四边形ABCD,且AB=12,CD=8,则四边形的周长是 .
③圆外切四边形的周长为48cm,相邻的三条边的比为5:4:7,求四边形各边的长.
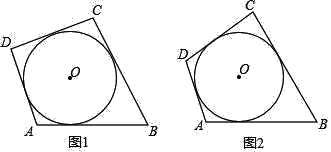
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平行四边形ABCD中,AB=5,BC=8,cosB=![]() ,点E是BC边上的动点,当以CE为半径的⊙C与边AD有两个交点时,半径CE的取值范围是( )
,点E是BC边上的动点,当以CE为半径的⊙C与边AD有两个交点时,半径CE的取值范围是( )
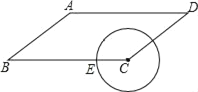
A. 0<CE≤8 B. 0<CE≤5 C. 3<CE≤8 D. 3<CE≤5
查看答案和解析>>
科目:初中数学 来源: 题型:
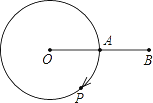
【题目】如图,A是半径为6cm的⊙O上的定点,动点P从A出发,以πcm/s的速度沿圆周按顺时针方向运动,当点P回到A时立即停止运动.设点P运动时间为t(s);
(1)当t=6s时,∠POA的度数是________;
(2)当t为多少时,∠POA=120°;
(3)如果点B是OA延长线上的一点,且AB=AO,问t为多少时,△POB为直角三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com