
【题目】如图,矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为_____.

【答案】3或6.
【解析】
当![]() 为直角三角形时,有两种情况:
为直角三角形时,有两种情况:
①当点![]() 落在矩形内部时,如答图1所示.
落在矩形内部时,如答图1所示.
连结![]() ,先利用勾股定理计算出
,先利用勾股定理计算出![]() ,根据折叠的性质得
,根据折叠的性质得![]() ,而当
,而当![]() 为直角三角形时,只能得到
为直角三角形时,只能得到![]() ,所以点
,所以点![]() 、
、![]() 、
、![]() 共线,即
共线,即![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在对角线
落在对角线![]() 上的点
上的点![]() 处,则
处,则![]() ,
,![]() ,可计算出
,可计算出![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,然后在
,然后在![]() 中运用勾股定理可计算出
中运用勾股定理可计算出![]() .
.
②当点![]() 落在
落在![]() 边上时,如答图2所示.此时四边形
边上时,如答图2所示.此时四边形![]() 为正方形.
为正方形.
解:当![]() 为直角三角形时,有两种情况:
为直角三角形时,有两种情况:
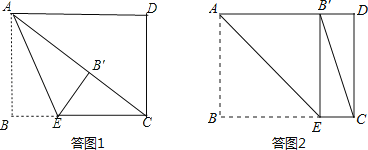
①当点![]() 落在矩形内部时,如答图1所示.
落在矩形内部时,如答图1所示.
连结![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在点
落在点![]() 处,
处,
![]() ,
,
当![]() 为直角三角形时,只能得到
为直角三角形时,只能得到![]() ,
,
![]() 点
点![]() 、
、![]() 、
、![]() 共线,即
共线,即![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在对角线
落在对角线![]() 上的点
上的点![]() 处,如图,
处,如图,
![]() ,
,![]() ,
,
![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
在![]() 中,
中,
![]() ,
,
![]() ,
,
解得![]() ,
,
![]() ;
;
②当点![]() 落在
落在![]() 边上时,如答图2所示.
边上时,如答图2所示.
此时![]() 为正方形,
为正方形,
![]() .
.
综上所述,![]() 的长为3或6.
的长为3或6.
故答案为:3或6.


科目:初中数学 来源: 题型:
【题目】2012年“国际攀岩比赛”在重庆举行.小丽从家出发开车前去观看,途中发现忘了带门票,于是打电话让妈妈马上从家里送来,同时小丽也往回开,遇到妈妈后聊了一会儿,接着继续开车前往比赛现场.设小丽从家出发后所用时间为t,小丽与比赛现场的距离为S.下面能反映S与t的函数关系的大致图象是( )
A.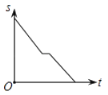 B.
B.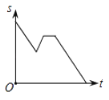 C.
C. D.
D.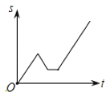
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+4经过点A(-1,0),B(4,0),与y轴交于点C,直线y=x+2交y轴于点D,交抛物线于E,F两点,点P为线段EF上一个动点(与E,F不重合),PQ∥y轴与抛物线交于点Q.
(1)求抛物线的解析式;
(2)当P在什么位置时,四边形PDCQ为平行四边形?求出此时点P的坐标;
(3)是否存在点P使△POB为等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明利用星期六、日双休骑自行车到城外小姨家去玩.星期六从家中出发,先上坡,后走平 路,再走下坡路到小姨家.行程情况如图所示.星期日小明又沿原路返回自己家.若两天中,小明 上坡、平路、下坡行驶的速度相对不变,则星期日,小明返回家的时间是( )分钟
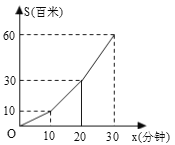
A.30 分钟B.38![]() 分钟C.41
分钟C.41![]() 分钟D.43
分钟D.43![]() 分钟
分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,![]() 是对角线,
是对角线,![]() 交
交![]() 延长线于
延长线于![]() .若四边形
.若四边形![]() 是菱形,则四边形
是菱形,则四边形![]() 是( )
是( )

A. 平行四边形 B. 矩形
C. 菱形 D. 正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
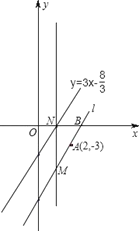
【题目】如图,在平面直角坐标系中,直线 l 经过点A(2,﹣3),与 x 轴交于点 B,且与直线y=3x-![]() 平行.
平行.
(1)求直线l的函数解析式及点B的坐标;
(2)如直线l上有一点 M(a,﹣6),过点 M 作 x 轴的垂线,交直线 y=3x-![]() 于点N,在线段MN上求一点P,使△PAB是直角三角形,请求出点P的坐标.
于点N,在线段MN上求一点P,使△PAB是直角三角形,请求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形的顶点A(1,1)、B(3,1),规定把等边△ABC“先沿x轴翻折,再向左平移1个单位”为一次变换,如果这样连续经过2018次变换后,等边△ABC的顶点C的坐标为_____.
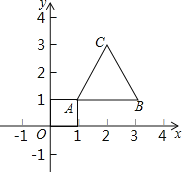
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在BC上,DE⊥AB于点E,DF⊥BC交AC于点F,BD=CF,BE=CD.若∠AFD=145°,则∠EDF=_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形ABCD在平面直角坐标系中的位置如图所示,其中A(﹣4,0),B(2,0),C(3,3)反比例函数![]() 的图象经过点C.
的图象经过点C.
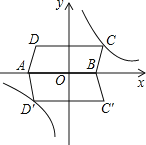
(1)求此反比例函数的解析式;
(2)将平行四边形ABCD沿x轴翻折得到平行四边形AD′C′B,请你通过计算说明点D′在双曲线上;
(3)请你画出△AD′C,并求出它的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com