【题目】如图，等边三角形的顶点A（1，1）、B（3，1），规定把等边△ABC“先沿x轴翻折，再向左平移1个单位”为一次变换，如果这样连续经过2018次变换后，等边△ABC的顶点C的坐标为_____．
心算口算巧算一课一练系列答案
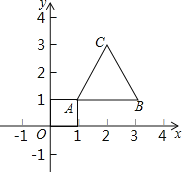
应用题作业本系列答案科目：初中数学 来源： 题型：
【题目】如图，A、B两个村庄的坐标分别为（2，2）、（7，4），一辆汽车从原点O出发，在x轴上行驶．
（1）汽车行驶到什么位置时离村庄A最近？写出此位置的坐标．
（2）汽车行驶到什么位置时离村庄B最近？写出此位置的坐标．
（3）请在图中画出汽车到两村庄的距离和最短的位置，并求出此最短的距离和．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，矩形ABCD中，AB＝6，BC＝8，点E是BC边上一点，连接AE，把∠B沿AE折叠，使点B落在点B′处，当△CEB′为直角三角形时，BE的长为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
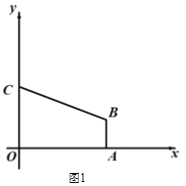
【题目】如图1，在平面直角坐标系中,直角梯形OABC的顶点A的坐标为(4，0)，直线y = -
x + 3经过顶点 B，与y轴交于顶点C，AB // OC.
(1)求顶点B的坐标.
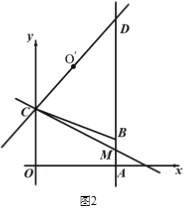
(2)如 图2，直线 L 经过点 C，与直线 AB 交于点 M，点 O′为点 O 关于直线L的对称点,联 结 CO′，并延长交直线AB于第一象限的点 D，当CD=5 时，求直线 L的解析式；
(3)在(2)条件下，点P在直线 L上运动，点Q在直线OD上运动，以 P、Q、B、C 为顶点的四边形能否成为平行四边形？若能,请直接写出点P坐标；若不能，说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，O是坐标原点，菱形OABC的顶点A（3，4），C在x轴的负半轴，抛物线y=﹣
（x﹣2）2+k过点A．
（1）求k的值；
（2）若把抛物线y=﹣
（x﹣2）2+k沿x轴向左平移m个单位长度，使得平移后的抛物线经过菱形OABC的顶点C．试判断点B是否落在平移后的抛物线上，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】)图①中是一座钢管混凝土系杆拱桥，桥的拱肋ACB可视为抛物线的一部分(如图②)，桥面(视为水平的)与拱肋用垂直于桥面的系杆连接，测得拱肋
的跨度AB为200米，与AB中点O相距20米处有一高度为48米的系杆．
【1】求正中间系杆OC的长度；
【2】若相邻系杆之间的间距均为5米(不考虑系杆的粗细)，则是否存在一根系杆的长度恰好是OC长度的一半？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，O为坐标原点，点A（a，a）在第一象限，点B（0，b），点C（3，0），
其中0＜b＜3，∠BAC＝90°．
（1）根据题意，画出示意图；
（2）若a＝2，求OB的长；
（3）已知点D在线段OB的上，若
，四边形OCAD的面积为3，求
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】对于三个数a，b，c，用max{a，b，c}表示这三个数中最大数，例如：max{-2，1，0}=1，max
解决问题：
（1）填空：max{1，2，3}=______，如果max{3，4，2x-6}=2x-6，则x的取值范围为______；
（2）如果max{2，x+2，-3x-7}=5，求x的值；
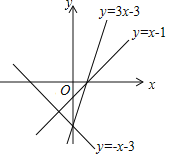
（3）如图，在同一坐标系中画出了三个一次函数的图象：y=-x-3，y=x-1和y=3x-3请观察这三个函数的图象，
①在图中画出max{-x-3，x-1，3x-3}对应的图象（加粗）；
②max{-x-3，x-1，3x-3}的最小值为______．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
