
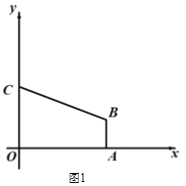
����Ŀ����ͼ1����ƽ��ֱ������ϵ��,ֱ������OABC�Ķ���A������Ϊ(4��0)��ֱ��y = -![]() x + 3�������� B����y�ύ�ڶ���C��AB // OC.
x + 3�������� B����y�ύ�ڶ���C��AB // OC.
(1)��B������.
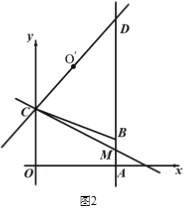
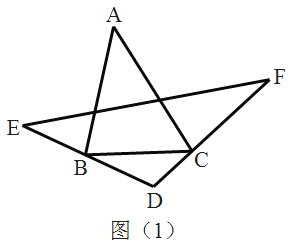
(2)�� ͼ2��ֱ�� L ������ C����ֱ�� AB ���ڵ� M���� O��Ϊ�� O ����ֱ��L�ĶԳƵ�,�� �� CO�������ӳ���ֱ��AB�ڵ�һ���ĵ� D����CD=5 ʱ����ֱ�� L�Ľ���ʽ��
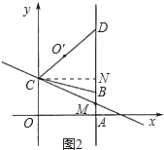
(3)��(2)�����£���P��ֱ�� L���˶�����Q��ֱ��OD���˶����� P��Q��B��C Ϊ������ı����ܷ��Ϊƽ���ı��Σ�����,��ֱ��д����P���ꣻ�����ܣ�˵������.
���𰸡���1��B(4,2)����2��![]() ����3��P������Ϊ��2,2����5,
����3��P��������2,2����5,![]() ����-2,4��.
����-2,4��.
��������
��1�������������B������Ϊ(4,y)����x=4����ֱ�߽���ʽ�������B�������꣬�Ӷ��õ�B�����ꣻ
��2����C����CN��AB��N����ƽ���ߺͶԳƵ����ʿ��Ƴ���DCM=��DMC�������õ�CD=MD=5�����ù��ɶ������DN���õ�NM=2����AM=1���Ӷ��õ�M�����꣬���ô���ϵ�����������ֱ��L�Ľ���ʽ��
��3������OD�������ODֱ�߽���ʽ�����ݵ�P��ֱ�� L���˶�����Q��ֱ��OD���˶�������P������Ϊ��![]() ����Q������Ϊ��
����Q������Ϊ��![]() �����ڷ������ۣ�����ƽ���ı��ζԽ�����ƽ�ֵ����ʺ��е����깫ʽ�ɽ����������.
�����ڷ������ۣ�����ƽ���ı��ζԽ�����ƽ�ֵ����ʺ��е����깫ʽ�ɽ����������.
�⣺(1)��A(4,0)��AB��OC��
�����B������Ϊ(4,y)
��x=4����![]() ����y=2��
����y=2��
��B(4,2)��
(2)��ͼ����C����CN��AB��N,
��AB��OC��
���OCM=��DMC��
�ߵ� O��Ϊ�� O ����ֱ��L�ĶԳƵ�
����DCM=��OCM��
���DCM=��DMC
��CD=MD=5��
��![]() ����x=0ʱy=3��
����x=0ʱy=3��
��OC=3��
��CN=OA=4��
��DN=![]() ��
��
��NM=53=2��
��AM=AN-NM=3-2=1
��M(4,1)��
��ֱ��L����ʽy=kx+b��C(0,3)��M(4,1)����ã�
![]() �����
�����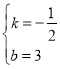 ��
��
��ֱ��L�Ľ���ʽΪ��![]() .
.
��3����ͼ������OD��
��AD=AM+MD=1+5=6��AD��OC��A��������4,0��
��D��������4,6��
��ODֱ�߽���ʽΪ![]() ������4,6������ɵ�
������4,6������ɵ�![]() �����
�����![]()
��ֱ��OD����ʽΪ![]() ��
��
�ߵ�P��ֱ�� L���˶�����Q��ֱ��OD���˶�
����P��������![]() ����Q��������
����Q��������![]() ����
����
��������ۣ�
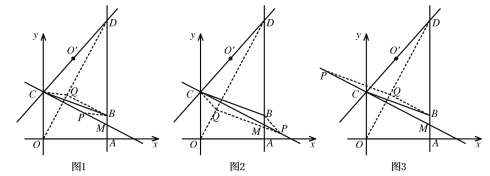
��ͼ1��ʾ����BC��PQΪ�Խ���ʱ����ƽ���ı��ζԽ�����ƽ�ֵ����ʺ��е����깫ʽ�ɵã�
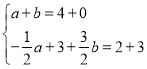 �����
�����![]() ��
��
��![]() ʱ��
ʱ��![]()
��P��������2,2����
��ͼ2��ʾ����BQ��PCΪ�Խ���ʱ��ͬ���ɵã�
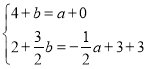 �����
�����![]() ��
��
��![]() ʱ��
ʱ��![]()
��P��������5,![]() ����
����
��ͼ3��ʾ����BP��CQΪ�Խ���ʱ��ͬ���ɵã�
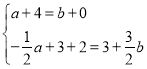 �����
�����![]() ��
��
��![]() ʱ��
ʱ��![]()
��P��������-2,4����
����������P����������2,2����5,![]() ����-2,4��.
����-2,4��.


 �Ͻ�ƽСѧ��������ϵ�д�
�Ͻ�ƽСѧ��������ϵ�д� �Ƹ������������ϵ�д�
�Ƹ������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ������
������![]() �ϣ�ʹ��
�ϣ�ʹ��![]() ��������
��������![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() .
.
��1������![]() ��ͼ��1��������
��ͼ��1��������![]() ��ʱ����
��ʱ����![]() �Ĵ�С��
�Ĵ�С��
��2������![]() ��ͼ��2��������
��ͼ��2��������![]() ��ʱ����
��ʱ����![]() �Ĵ�С.
�Ĵ�С.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
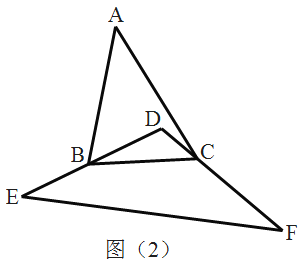
����Ŀ����ͼ����������![]() �У���
�У���![]() ��һֱ����
��һֱ����![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ����
����![]() ��
��![]() ��ֱ
��ֱ![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() ��ֱ
��ֱ![]() �ڵ�
�ڵ�![]() ����
����![]() �Ͻ�ȡ
�Ͻ�ȡ![]() ���ٹ�
���ٹ�![]() ��
��![]() ��ֱ
��ֱ![]() ��
��![]() ��
��![]() ����
����![]() ����
����![]() ���ı���
���ı���![]() �����֮��Ϊ________��
�����֮��Ϊ________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��![]() �У�
��![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() ���е㣬
���е㣬![]() �ǶԽ��ߣ�
�ǶԽ��ߣ�![]() ��
��![]() �ӳ�����
�ӳ�����![]() �����ı���
�����ı���![]() �����Σ����ı���
�����Σ����ı���![]() �ǣ� ��
�ǣ� ��

A. ƽ���ı��� B. ����
C. ���� D. ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
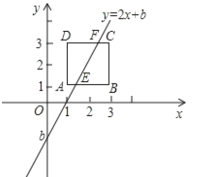
����Ŀ����ͼ����֪������ABCD�Ķ���A(1��1)��B(3��1)��ֱ��y=2x+b����AB�ڵ�E������CD�ڵ�F����ֱ��y=2x+b ��y ���ϵĽؾ�b�ı仯��Χ��__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ȱ������εĶ���A��1��1����B��3��1�����涨�ѵȱߡ�ABC������x�ᷭ�ۣ�������ƽ��1����λ��Ϊһ�α任�����������������2018�α任�ȱߡ�ABC�Ķ���C������Ϊ_____��
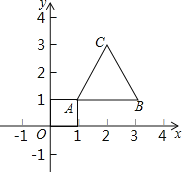
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
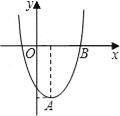
����Ŀ����ֱ������ƽ���ڣ����κ���ͼ��Ķ���ΪA��1����4�����ҹ���B��3��0����
��1����ö��κ����Ľ���ʽ��
��2�����ö��κ���ͼ������ƽ�Ƽ�����λ����ʹƽ�ƺ�����ͼ������ԭ�㣿��ֱ��д��ƽ�ƺ�����ͼ����x�����һ����������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��ͼ��������һ��ֱ�߽�����ԳƱ任��������������ֱ��ƽ�еķ���ƽ�ƣ����ǰ�������ͼ�α任���������ԳƱ任�������ԳƱ任��ƽ�Ʊ任���й����ʣ�����Ϊ�ڻ����ԳƱ任�����У���������Ӧ������(��ͼ)�Ķ�Ӧ�������е�������( ).

A. ��Ӧ�������߶ζ���� B. ��Ӧ�������߶α��Գ���ƽ��
C. ��Ӧ��������Գ��ᴹֱ D. ��Ӧ��������ƽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��������ʻʱ�ĺ�����Ϊ0.1��/ǧ�ף���ͼ������ʣ������![]() ���������ڼ����ͺ�����ʻ��·��
���������ڼ����ͺ�����ʻ��·��![]() ��ǧ�ף��ĺ���ͼ��.
��ǧ�ף��ĺ���ͼ��.

��1������ͼ��ֱ��д��������ʻ400ǧ��ʱ�������ڵ�ʣ�������������������ʱ�����������
��2����![]() ����
����![]() �ĺ�����ϵʽ���������������ʣ������5��ʱ������ʻ��·��.
�ĺ�����ϵʽ���������������ʣ������5��ʱ������ʻ��·��.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com