
【题目】如图,在正方形![]() 中,过
中,过![]() 作一直线与
作一直线与![]() 相交于点
相交于点![]() ,过
,过![]() 作
作![]() 垂直
垂直![]() 于点
于点![]() ,过
,过![]() 作
作![]() 垂直
垂直![]() 于点
于点![]() ,在
,在![]() 上截取
上截取![]() ,再过
,再过![]() 作
作![]() 垂直
垂直![]() 交
交![]() 于
于![]() .若
.若![]() .则
.则![]() 与四边形
与四边形![]() 的面积之和为________.
的面积之和为________.

【答案】9
【解析】
由ABCD为正方形,根据正方形的性质得到AB=BC,∠ABC=90°,即∠CBG+∠ABF=90°,又根据CG与BE垂直得到∠BCG+∠CBG=90°,根据同角的余角相等得到一对角相等,又根据一对直角相等,利用“AAS”即可得到三角形BCG与三角形FBA全等,根据全等三角形的对应边相等得到AF与BG相等,又因为FH=FB,从而得到AH=FG,然后由垂直得到一对直角相等,加上一个公共角,得到三角形APH与三角形ABF相似,根据相似得比例,设AH=FG=x,用x表示出PH,由四边形PHFB一组对边平行,另一组对边不平行得到此四边形为梯形,根据梯形的面积公式,由上底PH,下底为BF=3,高FH=3,表示出梯形的面积;然后在三角形BCG与三角形ECG中,根据同角的余角相等,再加上一对直角得到两三角形相似,根据相似得比例,用含x的式子表示出GE,由CG=3,表示出的GE,利用三角形的面积公式表示出直角三角形CGE的面积,把表示出的两面积相加,化简即可得到结论.
∵四边形ABCD为正方形,∴AB=BC,∠ABC=90°,即∠CBG+∠ABF=90°,又CG⊥BE,即∠BGC=90°,∴∠BCG+∠CBG=90°,∴∠ABF=∠BCG,又AF⊥BG,∴∠AFB=∠BGC=90°,∴△ABF≌△BCG,∴AF=BG,BF=CG=FH=3.
又∵FH=BF,∴AH=FG,设AH=FG=x.
∵PH⊥AF,BF⊥AF,∴∠AHP=∠AFB=90°,又∠PAH为公共角,∴△APH∽△ABF,∴![]() =
=![]() ,即PH=
,即PH=![]() .
.
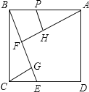
∵PH∥BF,BP不平行FH,∴四边形BFHP为梯形,其面积为![]() =
=![]() +
+![]() ;
;
又∵∠BCG+∠ECG=90°,∠ECG+∠BEC=90°,∴∠BCG=∠BEC,又∠BGC=∠CGE=90°,∴△BCG∽△CEG,∴![]() =
=![]() ,即GE=
,即GE=![]() ,故Rt△CGE的面积为
,故Rt△CGE的面积为![]() ×3×
×3×![]() ,则△CGE与四边形BFHP的面积之和为
,则△CGE与四边形BFHP的面积之和为![]() +
+![]() +
+![]() =
=![]() +
+![]() =9.
=9.
故答案为:9.


科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,黔南州近期举办了中小学生“国学经典大赛”,比赛项目为:A.唐诗;B.宋词;C.论语;D.三字经.比赛形式为两人对抗赛,即把四种比赛项目写在4张完全相同的卡片上,比赛时,比赛的两人从中随机抽取1张卡片作为自己的比赛项目(不放回,且每人只能抽取一次)比赛时,小红和小明分到一组.(1)小明先抽取,那么小明抽到唐诗的概率是多少?
(2)小红擅长唐诗,小红想:“小明先抽取,我后抽取”抽到唐诗的概率是不同的,且小明抽到唐诗的概率更大,若小红后抽取,小红抽中唐诗的概率是多少?小红的想法对吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车同时分别从 A,B 两处出发,沿直线 AB 作匀速运动,同时到达C 处,B 在 AC 上,甲的速度是乙的速度的1.5 倍,设 t(分)后甲、 乙两遥控车与 B 处的距离分别为 d1,d2,且 d1,d2 与出发时间 t 的函数关系如图,那么在两车相遇前,两车与 B 点的距离相等时,t 的值为( )
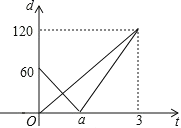
A.0.4B.0.5C.0.6D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DE、FG相交于点H.

(1)判断线段DE、FG的位置关系,并说明理由;
(2)连结CG,求证:四边形CBEG是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣2x+4与x轴,y轴分别交于A,B,以线段AB为直角边在第一象限内作Rr△ABC,使AB=AC.
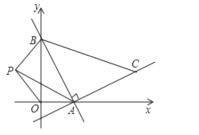
(1)点A的坐标是 ,点B的坐标是 ;
(2)求直线AC的函数关系式;
(3)若P(m,3)在第二象限内,求当△PAB与△ABC面积相等时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,正方形OABC的顶点O与原点重合,顶点A。C分别在x轴、y轴上,反比例函数![]() 的图象与正方形的两边AB、BC分别交于点M、N,ND⊥x轴,垂足为D,连接OM、ON、MN。
的图象与正方形的两边AB、BC分别交于点M、N,ND⊥x轴,垂足为D,连接OM、ON、MN。
下列结论:
①△OCN≌△OAM;
②ON=MN;
③四边形DAMN与△MON面积相等;
④若∠MON=450,MN=2,则点C的坐标为![]() 。
。
其中正确的个数是【 】

A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
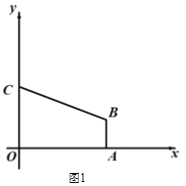
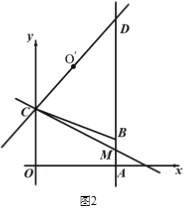
【题目】如图1,在平面直角坐标系中,直角梯形OABC的顶点A的坐标为(4,0),直线y = -![]() x + 3经过顶点 B,与y轴交于顶点C,AB // OC.
x + 3经过顶点 B,与y轴交于顶点C,AB // OC.
(1)求顶点B的坐标.
(2)如 图2,直线 L 经过点 C,与直线 AB 交于点 M,点 O′为点 O 关于直线L的对称点,联 结 CO′,并延长交直线AB于第一象限的点 D,当CD=5 时,求直线 L的解析式;
(3)在(2)条件下,点P在直线 L上运动,点Q在直线OD上运动,以 P、Q、B、C 为顶点的四边形能否成为平行四边形?若能,请直接写出点P坐标;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知A,B,C三点的坐标分别为(0,a)(b,0)(b,c)(如图所示),其中a,b,c满足关系式(a﹣2)2+![]() =0,|c﹣4|≤0.
=0,|c﹣4|≤0.

(1)求a,b,c的值;
(2)如果在第二象限内有一点P(m,1),请用含m的代数式表示的面积;
(3)在(2)的条件下,是否存在点P,使△AOP的面积与△ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com