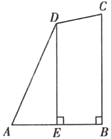
【题目】如图，在四边形
中，
为
的中点，
于点，
，
，
，则
的大小为______.（提示：一个三角形中有两条边相等，那么这两条边所对的角也相等）
【答案】
【解析】
由E是AB中点可得AE=BE，由DE⊥AB可得∠AED=∠BED=90°，理由SAS可证明△AED≌△BED，可得BD=AD，∠EBD=∠A，可求出∠DBC的度数，根据AD=BC可得BC=BD，即可得出∠C=∠BDC，根据三角形内角和定理求出∠C的度数即可.
∵E是AB中点，
∴AE=BE，
∵DE⊥AB，
∴∠AED=∠BED=90°，
在△AED和△BED中，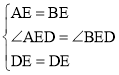
，
∴△AED≌△BED，
∴BD=AD，∠EBD=∠A=66°，
∵∠ABC=90°，
∴∠DBC=90°-66°=24°，
∵AD=BC，
∴BD=BC，
∴∠C=∠BDC=
（180°-∠DBC）=78°.
故答案为：78°
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】已知，ACB和DCE都是等腰直角三角形，∠ACB=∠DCE=90
，连接AE、BD交于点O. AE与DC交于点M，BD与AC交于点N.
（1）如图①，求证：AE=BD；
（2）如图②，若AC=DC，在不添加任何辅助线的情况下，请直接写出图②中四对全等的直角三角形.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在
中，
，
，点
是
边所在直线上的一个动点，
与交于点，
与
边所在直线交于点
．
在图①中，
，直接写出
的值；
在图②中，
，直接写出的值；
在图③中，，先写出的值，再加以证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，抛物线y＝ax2＋bx＋4经过点A(－1，0)，B(4，0)，与y轴交于点C，直线y＝x＋2交y轴于点D，交抛物线于E，F两点，点P为线段EF上一个动点(与E，F不重合)，PQ∥y轴与抛物线交于点Q.
(1)求抛物线的解析式；
(2)当P在什么位置时，四边形PDCQ为平行四边形？求出此时点P的坐标；
(3)是否存在点P使△POB为等腰三角形？若存在，请直接写出点P的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明利用星期六、日双休骑自行车到城外小姨家去玩.星期六从家中出发，先上坡，后走平 路,再走下坡路到小姨家.行程情况如图所示.星期日小明又沿原路返回自己家.若两天中，小明 上坡、平路、下坡行驶的速度相对不变，则星期日，小明返回家的时间是( )分钟
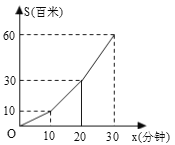
A.30 分钟B.38
分钟C.41
分钟D.43分钟
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知在
中，
，
分别是
，
的中点，
是对角线，
交
延长线于
．若四边形
是菱形，则四边形
是（ ）
A. 平行四边形 B. 矩形
C. 菱形 D. 正方形
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，等边三角形的顶点A（1，1）、B（3，1），规定把等边△ABC“先沿x轴翻折，再向左平移1个单位”为一次变换，如果这样连续经过2018次变换后，等边△ABC的顶点C的坐标为_____．
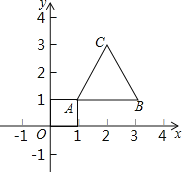
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知动点A在函数y=
（x＞0）的图象上，AB⊥x轴于点B，AC⊥y轴于点C，延长CA至点D，使AD=AB，延长BA至点E，使AE=AC，直线DE分别交x轴，y轴于点P，Q，当QE：DP=9：25时，图中的阴影部分的面积等于___．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
