
【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边所在直线上的一个动点,
边所在直线上的一个动点,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 边所在直线交于点
边所在直线交于点![]() .
.
![]() 在图①中,
在图①中,![]() ,直接写出
,直接写出![]() 的值;
的值;
![]() 在图②中,
在图②中,![]() ,直接写出
,直接写出![]() 的值;
的值;
![]() 在图③中,
在图③中,![]() ,先写出
,先写出![]() 的值,再加以证明.
的值,再加以证明.

【答案】(1)![]() ;(2)2;(3)
;(2)2;(3)![]()
【解析】
(1)过D作DF⊥BC于F,在△ABC中,∠ABC=90°,AB=BC,得到∠ACB=45°,于是得到DF=CF,根据AB∥DF,得到比例式![]() ,设DF=CF=2k,则AC=BC=3k,通过△BDF∽△DEF,即可得到结论;
,设DF=CF=2k,则AC=BC=3k,通过△BDF∽△DEF,即可得到结论;
(2)过D作DF⊥BC于F,同理△CDF是等腰直角三角形,通过△ABC≌△DFC,得到AB=DF,BC=CF于是得到BF=2DF,由(1)证得△BDF∽△DEF,列比例式即可得到结论;
(3)![]() ,如图③过D作DF⊥BC于F,首先证得△DFC是等腰直角三角形,再通过三角形相似得到
,如图③过D作DF⊥BC于F,首先证得△DFC是等腰直角三角形,再通过三角形相似得到![]() ,设AB=k,DF=2k,则BC=k,CF=2k,然后由△BDF∽△DEF得到结论
,设AB=k,DF=2k,则BC=k,CF=2k,然后由△BDF∽△DEF得到结论![]() .
.
![]() 过
过![]() 作
作![]() 于
于![]() ,
,

∵在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
![]() 过
过![]() 作
作![]() 于
于![]() ,
,

同理![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 与
与![]() 中,
中, ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
由![]() 证得
证得![]() ,
,
∴![]() ;
;
![]() ,
,
如图③,

过![]() 作
作![]() 于
于![]() ,
,
∵在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】某商场将进货价为40元的台灯以50元的销售价售出,平均每月能售出800个.市场调研表明:当销售价每上涨1元时,其销售量就将减少10个.设每个台灯的销售价上涨![]() 元.
元.
(1) 试用含![]() 的代数式填空:
的代数式填空:
①涨价后,每个台灯的利润为 元;
②涨价后,商场的台灯平均每月的销售量为 台;
(2) 如果商场要想销售总利润平均每月达到20000元,商场经理甲说“在原售价每台50元的基础上再上涨40元,可以完成任务”,商场经理乙说“不用涨那么多,在原售价每台50元的基础上再上涨30元就可以了”,试判断经理甲与乙的说法是否正确,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B两个村庄的坐标分别为(2,2)、(7,4),一辆汽车从原点O出发,在x轴上行驶.
(1)汽车行驶到什么位置时离村庄A最近?写出此位置的坐标.
(2)汽车行驶到什么位置时离村庄B最近?写出此位置的坐标.
(3)请在图中画出汽车到两村庄的距离和最短的位置,并求出此最短的距离和.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车同时分别从 A,B 两处出发,沿直线 AB 作匀速运动,同时到达C 处,B 在 AC 上,甲的速度是乙的速度的1.5 倍,设 t(分)后甲、 乙两遥控车与 B 处的距离分别为 d1,d2,且 d1,d2 与出发时间 t 的函数关系如图,那么在两车相遇前,两车与 B 点的距离相等时,t 的值为( )
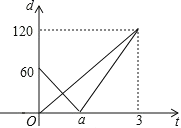
A.0.4B.0.5C.0.6D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是 ( )

A. ![]() B. 2
B. 2![]() C. 3 D. 2
C. 3 D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DE、FG相交于点H.

(1)判断线段DE、FG的位置关系,并说明理由;
(2)连结CG,求证:四边形CBEG是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】)图①中是一座钢管混凝土系杆拱桥,桥的拱肋ACB可视为抛物线的一部分(如图②),桥面(视为水平的)与拱肋用垂直于桥面的系杆连接,测得拱肋
的跨度AB为200米,与AB中点O相距20米处有一高度为48米的系杆.
【1】求正中间系杆OC的长度;
【2】若相邻系杆之间的间距均为5米(不考虑系杆的粗细),则是否存在一根系杆的长度恰好是OC长度的一半?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com