
【题目】如图,∠BAD=∠CAE=90o,AB=AD,AE=AC.
(1)若AC=10,求四边形ABCD的面积;
(2)求证:AC平分∠ECF;

【答案】(1)50(2)见解析
【解析】
(1)求出∠BAC=∠EAD,根据SAS推出△ABC≌△ADE,推出四边形ABCD的面积=三角形ACE的面积,即可得出答案;
(2)根据等腰直角三角形的性质得出∠ACE=∠AEC=45°,△ABC≌△ADE求出∠ACB=∠AEC=45°,推出∠ACB=∠ACE即可;
(1)∵∠BAD=∠CAE=90°,
∴∠BAC+∠CAD=∠EAD+∠CAD
∴∠BAC=∠EAD,
在△ABC和△ADE中,
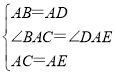 ,
,
∴△ABC≌△ADE(SAS),
∵S四边形ABCD=S△ABC+S△ACD,
∴S四边形ABCD=S△ADE+S△ACD=S△ACE=![]() ×102=50;
×102=50;
(2)证明:∵△ACE是等腰直角三角形,
∴∠ACE=∠AEC=45°,
由△ABC≌△ADE得:
∠ACB=∠AEC=45°,
∴∠ACB=∠ACE,
∴AC平分∠ECF.


科目:初中数学 来源: 题型:
【题目】如果一个三位数,十位数字等于百位数字与个位数字的平均数,我们称这个三位数为“顺子数”,例如:630,123.
如果一个三位数,十位数字等于百位数字与个位数字的积的算术平方根,我们称这个三位数为“和谐数”,例如:139,124.
(1)若三位数![]() 是“顺子数”,且各位数字之和大于7小于10,且百位数字a使得一元二次方程(a﹣5)x2+2ax+a﹣6=0有实数根,求这个“顺子数”;
是“顺子数”,且各位数字之和大于7小于10,且百位数字a使得一元二次方程(a﹣5)x2+2ax+a﹣6=0有实数根,求这个“顺子数”;
(2)若三位数![]() 既是“顺子数”又是“和谐数”,请探索a,b,c三者的关系.
既是“顺子数”又是“和谐数”,请探索a,b,c三者的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD=BC=12,AB=CD,BD=15,点E从D点出发,以每秒4个单位的速度沿D→A→D匀速移动,点F从点C出发,以每秒1个单位的速度沿CB向点B作匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动,假设移动时间为t秒.

(1)试说明:AD∥BC;
(2)在移动过程中,小明发现有△DEG与△BFG全等的情况出现,请你探究这样的情况会出现几次?并分别求出此时的移动时间t和G点的移动距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,ACB和DCE都是等腰直角三角形,∠ACB=∠DCE=90![]() ,连接AE、BD交于点O. AE与DC交于点M,BD与AC交于点N.
,连接AE、BD交于点O. AE与DC交于点M,BD与AC交于点N.
(1)如图①,求证:AE=BD;
(2)如图②,若AC=DC,在不添加任何辅助线的情况下,请直接写出图②中四对全等的直角三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=45°,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,且EH=EB.下列四个结论:①∠ABC=45°;②AH=BC;③BE+CH=AE;④△AEC是等腰直角三角形.你认为正确的序号是( )

A. ①②③ B. ①③④ C. ②③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2012年“国际攀岩比赛”在重庆举行.小丽从家出发开车前去观看,途中发现忘了带门票,于是打电话让妈妈马上从家里送来,同时小丽也往回开,遇到妈妈后聊了一会儿,接着继续开车前往比赛现场.设小丽从家出发后所用时间为t,小丽与比赛现场的距离为S.下面能反映S与t的函数关系的大致图象是( )
A.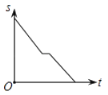 B.
B.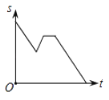 C.
C. D.
D.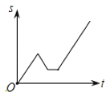
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边所在直线上的一个动点,
边所在直线上的一个动点,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 边所在直线交于点
边所在直线交于点![]() .
.
![]() 在图①中,
在图①中,![]() ,直接写出
,直接写出![]() 的值;
的值;
![]() 在图②中,
在图②中,![]() ,直接写出
,直接写出![]() 的值;
的值;
![]() 在图③中,
在图③中,![]() ,先写出
,先写出![]() 的值,再加以证明.
的值,再加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,![]() 是对角线,
是对角线,![]() 交
交![]() 延长线于
延长线于![]() .若四边形
.若四边形![]() 是菱形,则四边形
是菱形,则四边形![]() 是( )
是( )

A. 平行四边形 B. 矩形
C. 菱形 D. 正方形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com