
【题目】如果一个三位数,十位数字等于百位数字与个位数字的平均数,我们称这个三位数为“顺子数”,例如:630,123.
如果一个三位数,十位数字等于百位数字与个位数字的积的算术平方根,我们称这个三位数为“和谐数”,例如:139,124.
(1)若三位数![]() 是“顺子数”,且各位数字之和大于7小于10,且百位数字a使得一元二次方程(a﹣5)x2+2ax+a﹣6=0有实数根,求这个“顺子数”;
是“顺子数”,且各位数字之和大于7小于10,且百位数字a使得一元二次方程(a﹣5)x2+2ax+a﹣6=0有实数根,求这个“顺子数”;
(2)若三位数![]() 既是“顺子数”又是“和谐数”,请探索a,b,c三者的关系.
既是“顺子数”又是“和谐数”,请探索a,b,c三者的关系.
【答案】(1)这个“顺子数”为333或432或630;(2)a=b=c.
【解析】
(1)根据根的判别式求出实数![]() 的取值范围,各位数字之和大于7小于10,则a+b+c=8或a+b+c=9,再根据“顺子数”的定义得到
的取值范围,各位数字之和大于7小于10,则a+b+c=8或a+b+c=9,再根据“顺子数”的定义得到![]() 即可得出a+c=6,分类讨论即可.
即可得出a+c=6,分类讨论即可.
(2)根据“顺子数”,“和谐数”的定义得到ac=b2,a+c=2b,整理即可.
(1)根据题意得:△=(2a)2﹣4(a﹣5)(a﹣6)≥0且![]()
解得:![]() 且
且![]()
∵各位数字之和大于7小于10,
∴a+b+c=8或a+b+c=9,
又∵![]()
∴a+c=![]() (舍去)或a+c=6,
(舍去)或a+c=6,
若a=3,则c=3,b=3,该数为333,
若a=4,则c=2,b=3,该数为432,
若a=6,则c=0,b=3,该数为630,
答:这个“顺子数”为333或432或630,
(2)根据题意得:
ac=b2,a+c=2b,
把![]() 代替ac=b2,得:
代替ac=b2,得:
![]()
整理得:a=c,
![]()
答:a,b,c三者的关系为:a=b=c.


科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程:x2﹣2(m+1)x+m2+5=0有两个不相等的实数根.
(1)求m的取值范围;
(2)若原方程的两个实数根为x1、x2, 且满足x12+x22=|x1|+|x2|+2x1x2,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售某种玩具,进货价为![]() 元.根据市场调查:在一段时间内,销售单价是
元.根据市场调查:在一段时间内,销售单价是![]() 元时,销售量是
元时,销售量是![]() 件,而销售单价每上涨
件,而销售单价每上涨![]() 元,就会少售出
元,就会少售出![]() 件玩具,超市要完成不少于
件玩具,超市要完成不少于![]() 件的销售任务,又要获得最大利润,则销售单价应定为________元.
件的销售任务,又要获得最大利润,则销售单价应定为________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+3的图象经过点 (-3,0),(2,-5).
(1)试确定此二次函数的解析式;
(2)请你判断点P(-2,3)是否在这个二次函数的图象上?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,下述结论:(1)BD平分∠ABC;(2)AD=BD=BC;(3)△BDC的周长等于AB+BC;(4)D是AC中点.其中正确的命题序号是( )
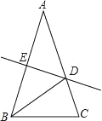
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,完成下列推理过程:
如图所示,点E在![]() 外部,点D在BC边上,DE交AC于F,若
外部,点D在BC边上,DE交AC于F,若![]() ,
,![]() ,
,
求证:![]() .
.

证明:∵![]() (已知),
(已知),
![]() (________________),
(________________),
∴![]() (________________),
(________________),
又∵![]() ,
,
∴________![]() ________
________![]() (________),
(________),
即![]() ,
,
在![]() 和
和![]() 中
中
![]() (已证)
(已证)
∵![]() (已知)
(已知)
![]() (已证)
(已证)
∴![]() (________).
(________).
∴![]() (________________)
(________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将直角三角板ABC绕直角顶点C逆时针旋转角度![]() ,得到△DCE,其中CE与AB交于点F,∠ABC=30°,连接BE,若△BEF为等腰三角形(即有两内角相等),则旋转角
,得到△DCE,其中CE与AB交于点F,∠ABC=30°,连接BE,若△BEF为等腰三角形(即有两内角相等),则旋转角![]() 的值为________.
的值为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进货价为40元的台灯以50元的销售价售出,平均每月能售出800个.市场调研表明:当销售价每上涨1元时,其销售量就将减少10个.设每个台灯的销售价上涨![]() 元.
元.
(1) 试用含![]() 的代数式填空:
的代数式填空:
①涨价后,每个台灯的利润为 元;
②涨价后,商场的台灯平均每月的销售量为 台;
(2) 如果商场要想销售总利润平均每月达到20000元,商场经理甲说“在原售价每台50元的基础上再上涨40元,可以完成任务”,商场经理乙说“不用涨那么多,在原售价每台50元的基础上再上涨30元就可以了”,试判断经理甲与乙的说法是否正确,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com