练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，已知在中，，分别是，的中点，是对角线，交延长线于．若四边形是菱形，则四边形是（ ）

    A. 平行四边形 B. 矩形

    C. 菱形 D. 正方形

    【答案】B

    【解析】

    如图：先由菱形的性质得出AE=BE=DE，通过AD∥BC，AG∥BD，可证明四边形ADBG是平行四边形，再通过角之间的关系求出∠2+∠3=90°即∠ADB=90°，所以判定四边形AGBD是矩形．

    ∵四边形ABCD是平行四边形，

    ∴AD∥BC．

    ∵AG∥BD，

    ∴四边形AGBD是平行四边形．

    ∵四边形BEDF是菱形，

    ∴DE=BE．

    ∵AE=BE，

    ∴AE=BE=DE．

    ∴∠1=∠2，∠3=∠4．

    ∵∠1+∠2+∠3+∠4=180°，

    ∴2∠2+2∠3=180°．

    ∴∠2+∠3=90°．

    即∠ADB=90°．

    ∴四边形AGBD是矩形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，∠BAD=∠CAE=90o，AB=AD，AE=AC.

    （1）若AC=10，求四边形ABCD的面积；

    （2）求证：AC平分∠ECF；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知Rt△ABC中，∠ABC=90°，先把△ABC绕点B顺时针旋转90°至△DBE后，再把△ABC沿射线平移至△FEG，DE、FG相交于点H．

    （1）判断线段DE、FG的位置关系，并说明理由；

    （2）连结CG，求证：四边形CBEG是正方形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在四边形中，为的中点，于点，，，，则的大小为______.（提示：一个三角形中有两条边相等，那么这两条边所对的角也相等）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在直角坐标系中，正方形OABC的顶点O与原点重合，顶点A。C分别在x轴、y轴上，反比例函数的图象与正方形的两边AB、BC分别交于点M、N，ND⊥x轴，垂足为D，连接OM、ON、MN。

    下列结论：

    ①△OCN≌△OAM；

    ②ON=MN；

    ③四边形DAMN与△MON面积相等；

    ④若∠MON=450，MN=2，则点C的坐标为。

    其中正确的个数是【 】

    　　A．1 　B．2　　 C．3　 　D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，矩形ABCD中，AB＝6，BC＝8，点E是BC边上一点，连接AE，把∠B沿AE折叠，使点B落在点B′处，当△CEB′为直角三角形时，BE的长为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

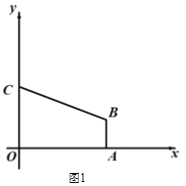
    【题目】如图1，在平面直角坐标系中,直角梯形OABC的顶点A的坐标为(4，0)，直线y = -x + 3经过顶点 B，与y轴交于顶点C，AB // OC.

    (1)求顶点B的坐标.

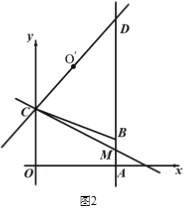
    (2)如 图2，直线 L 经过点 C，与直线 AB 交于点 M，点 O′为点 O 关于直线L的对称点,联 结 CO′，并延长交直线AB于第一象限的点 D，当CD=5 时，求直线 L的解析式；

    (3)在(2)条件下，点P在直线 L上运动，点Q在直线OD上运动，以 P、Q、B、C 为顶点的四边形能否成为平行四边形？若能,请直接写出点P坐标；若不能，说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】)图①中是一座钢管混凝土系杆拱桥，桥的拱肋ACB可视为抛物线的一部分(如图②)，桥面(视为水平的)与拱肋用垂直于桥面的系杆连接，测得拱肋

    的跨度AB为200米，与AB中点O相距20米处有一高度为48米的系杆．

    【1】求正中间系杆OC的长度；

    【2】若相邻系杆之间的间距均为5米(不考虑系杆的粗细)，则是否存在一根系杆的长度恰好是OC长度的一半？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，在平面直角坐标系中，A（m，0）、B（0，n），m、n满足(m-n)2+|m-|=0．C为AB的中点，P是线段AB上一动点，D是x轴正半轴上一点，且PO＝PD，DE⊥AB于E．

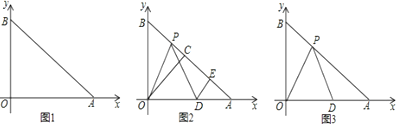
    （1）求∠OAB的度数；

    （2）设AB＝4，当点P运动时，PE的值是否变化？若变化，说明理由；若不变，请求PE的值；

    （3）设AB＝4，若∠OPD＝45°，求点D的坐标．

    查看答案和解析>>

    同步练习册答案