
【题目】如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DE、FG相交于点H.

(1)判断线段DE、FG的位置关系,并说明理由;
(2)连结CG,求证:四边形CBEG是正方形.
【答案】见解析
【解析】试题分析: (1)根据旋转和平移可得∠DEB=∠ACB,∠GFE=∠A,再根据∠ABC=90°可得∠A+∠ACB=90°,进而得到∠DEB+∠GFE=90°,从而得到DE、FG的位置关系是垂直;(2)根据旋转和平移找出对应线段和角,然后再证明是矩形,后根据邻边相等可得四边形CBEG是正方形.
试题解析:
(1)解:FG⊥ED.理由如下:
∵△ABC绕点B顺时针旋转90°至△DBE后,∴∠DEB=∠ACB,
∵把△ABC沿射线平移至△FEG,∴∠GFE=∠A,∵∠ABC=90°,
∴∠A+∠ACB=90°,∴∠DEB+∠GFE=90°,∴∠FHE=90°,∴FG⊥ED;
(2)证明:根据旋转和平移可得∠GEF=90°,∠CBE=90°,CG∥EB,CB=BE,
∵CG∥EB,∴∠BCG=∠CBE=90°,∴四边形BCGE是矩形,∵CB=BE,
∴四边形CBEG是正方形.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 相似三角形一定全等B. 不相似的三角形不一定全等
C. 全等三角形不一定是相似三角形D. 全等三角形一定是相似三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=k1x+b1与反比例函数y=![]() 的图象及坐标轴依次相交于A、B、C、D四点,且点A坐标为(﹣3,
的图象及坐标轴依次相交于A、B、C、D四点,且点A坐标为(﹣3,![]() ),点B坐标为(1,n).
),点B坐标为(1,n).
(1)求反比例函数及一次函数的解析式;
(2)求证:AC=BD;
(3)若将一次函数的图象上下平移若干个单位后得到y=k1x+n,其与反比例函数图象及两坐标轴的交点仍然依次为A、B、C、D.(2)中的结论还成立吗?请写出理由,对于任意k<0的直线y=kx+b.(2)中的结论还成立吗?(请直接写出结论)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去年12月24日全国大约有123万人参加研究生招生考试,123万这个数用科学记数法表示为( )
A. 1.23×106B. 1.23×107C. 0.123×107D. 12.3×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某运输队要运300 t物资到江边防洪.
(1)运输时间t(单位:h)与运输速度v(单位:t/h)之间有怎样的函数关系式?
(2)运了一半时,接到防洪指挥部命令,剩下的物资要在2 h之内运到江边,则运输速度至少为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
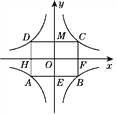
【题目】如图,是由四条曲线围成的广告标志,建立平面直角坐标系,双曲线对应的函数表达式分别为y=-![]() ,y=
,y=![]() .现用四根钢条固定这四条曲线,这种钢条加工成长方形产品按面积计算,每单位面积25元,请你帮助工人师傅计算一下,所需钢条一共花多少钱?
.现用四根钢条固定这四条曲线,这种钢条加工成长方形产品按面积计算,每单位面积25元,请你帮助工人师傅计算一下,所需钢条一共花多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中, ∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB于点E,AB=18cm,则△DBE的周长为( )
A. 16cm B. 8cm C. 18cm D. 10cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A和B两点在线段EF的中垂线上,且∠EBF=100°,∠EAF=70°,则∠AEB等于( )
A. 95° B. 15° C. 95°或15° D. 170°或30°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com