
【题目】已知,在平面直角坐标系中,A(m,0)、B(0,n),m、n满足(m-n)2+|m-![]() |=0.C为AB的中点,P是线段AB上一动点,D是x轴正半轴上一点,且PO=PD,DE⊥AB于E.
|=0.C为AB的中点,P是线段AB上一动点,D是x轴正半轴上一点,且PO=PD,DE⊥AB于E.
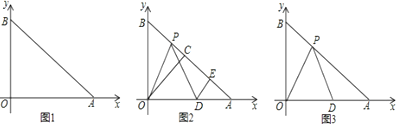
(1)求∠OAB的度数;
(2)设AB=4,当点P运动时,PE的值是否变化?若变化,说明理由;若不变,请求PE的值;
(3)设AB=4,若∠OPD=45°,求点D的坐标.
【答案】(1)∠OAB=45°.(2)![]()
【解析】
(1)根据非负数的性质即可求得a,b的值,从而得到△AOB是等腰直角三角形,据此即可求得;
(2)根据等腰三角形的性质以及三角形的外角的性质可以得到∠POC=∠DPE,即可证得△POC≌△DPE,则OC=PE,OC的长度根据等腰直角三角形的性质可以求得;
(3)利用等腰三角形的性质,以及外角的性质证得∠POC=∠DPE,即可证得△POC≌△DPE,根据全等三角形的对应边相等,即可求得OD的长,从而求得D的坐标.
解:(1)根据题意得:
 ,
,
解得:m=n=![]() ,
,
∴OA=OB, 又∵∠AOB=90°
∴△AOB为等腰直角三角形,
∴∠OAB=45°.
(2)PE的值不变.理由如下:
∵△AOB为等腰直角三角形,且AC=BC, ∴∠AOC=∠BOC=45°
又∵OC⊥AB于C, ∵PO=PD ∴∠POD=∠PDO
当P在BC上时,
∵∠POD=45°+∠POC,∠PDO=45°+∠DPE,
∴∠POC=∠DPE
在△POC和△DPE中,

∴△POC≌△DPE,∴OC=PE
又![]() ∴PE=2;
∴PE=2;
当P在AC上时,∠POD=45°﹣∠POC,∠PDO=45°﹣∠DPE,
则∠POC=∠DPE.
同理可得PE=2;
(3)∵OP=PD,
∴![]() ,
,
则∠PDA=180°﹣∠PDO=180°﹣67.5°=112.5°,
∵∠POD=∠A+∠APD,
∴∠APD=67.5°﹣45°=22.5°,
∴∠BPO=180°﹣∠OPD﹣∠APD=112.5°,
∴∠PDA=∠BPO
则在△POB和△DPA中,

∴△POB≌△DPA(AAS).
∴PA=OB=![]() ,
,
∴DA=PB=![]()
∴OD=OA﹣DA=![]()
∴ ![]()



科目:初中数学 来源: 题型:
【题目】如图,已知在![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,![]() 是对角线,
是对角线,![]() 交
交![]() 延长线于
延长线于![]() .若四边形
.若四边形![]() 是菱形,则四边形
是菱形,则四边形![]() 是( )
是( )

A. 平行四边形 B. 矩形
C. 菱形 D. 正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一个图形先沿着一条直线进行轴对称变换,再沿着与这条直线平行的方向平移,我们把这样的图形变换叫做滑动对称变换.结合轴对称变换和平移变换的有关性质,你认为在滑动对称变换过程中,这两个对应三角形(如图)的对应点所具有的性质是( ).

A. 对应点所连线段都相等 B. 对应点所连线段被对称轴平分
C. 对应点连线与对称轴垂直 D. 对应点连线互相平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知动点A在函数y=![]() (x>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC,直线DE分别交x轴,y轴于点P,Q,当QE:DP=9:25时,图中的阴影部分的面积等于___.
(x>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC,直线DE分别交x轴,y轴于点P,Q,当QE:DP=9:25时,图中的阴影部分的面积等于___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() (m为常数,且m≠5).
(m为常数,且m≠5).
(1)若在其图象的每个分支上,y随x的增大而增大,求m的取值范围;
(2)若其图象与一次函数y=-x+1的图象的一个交点的纵坐标是3,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形ABCD在平面直角坐标系中的位置如图所示,其中A(﹣4,0),B(2,0),C(3,3)反比例函数![]() 的图象经过点C.
的图象经过点C.
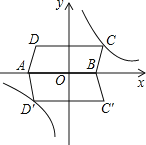
(1)求此反比例函数的解析式;
(2)将平行四边形ABCD沿x轴翻折得到平行四边形AD′C′B,请你通过计算说明点D′在双曲线上;
(3)请你画出△AD′C,并求出它的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车行驶时的耗油量为0.1升/千米,如图是油箱剩余油量![]() (升)关于加满油后已行驶的路程
(升)关于加满油后已行驶的路程![]() (千米)的函数图象.
(千米)的函数图象.

(1)根据图象,直接写出汽车行驶400千米时,油箱内的剩余油量,并计算加满油时油箱的油量;
(2)求![]() 关于
关于![]() 的函数关系式,并计算该汽车在剩余油量5升时,已行驶的路程.
的函数关系式,并计算该汽车在剩余油量5升时,已行驶的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】适逢中高考期间,某文具店平均每天可卖出![]() 支
支![]() 铅笔,卖出
铅笔,卖出![]() 支铅笔的利润是
支铅笔的利润是![]() 元,经调查发现,零售单价毎降
元,经调查发现,零售单价毎降![]() 元,每天可多卖出
元,每天可多卖出![]() 支铅笔,为了使每天获取的利润更多,该文具店决定把零售单价下降
支铅笔,为了使每天获取的利润更多,该文具店决定把零售单价下降![]() 元
元![]()
![]() 零售单价下降
零售单价下降![]() 元后,该文具店平均每天可卖出________支铅笔,总利润为________元.
元后,该文具店平均每天可卖出________支铅笔,总利润为________元.
![]() 在不考虑其他因素的条件下,当
在不考虑其他因素的条件下,当![]() 定为多少元时,才能使该文具店每天卖
定为多少元时,才能使该文具店每天卖![]() 铅笔获取的利润为
铅笔获取的利润为![]() 元?
元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰RtABC 中,∠BAC=90°,在BC上截取BD=BA,作∠ABC的平分线与AD相交于点P,连接PC,若△ABC的面积为8cm2,则△BPC的面积为( )

A. 4cm2 B. 5cm2 C. 6cm2 D. 7cm2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com