
【题目】如图,一次函数y=﹣2x+4与x轴,y轴分别交于A,B,以线段AB为直角边在第一象限内作Rr△ABC,使AB=AC.
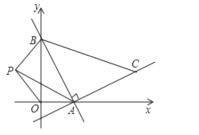
(1)点A的坐标是 ,点B的坐标是 ;
(2)求直线AC的函数关系式;
(3)若P(m,3)在第二象限内,求当△PAB与△ABC面积相等时m的值.
【答案】(1)(2,0),(0,4);(2)直线AC的解析式为:y=![]() x-1;(3)m=-
x-1;(3)m=-![]() .
.
【解析】
(1)令x=0和y=0分别代入y=-2x+4中即可求出A与B的坐标.
(2)过点C作CD⊥x轴于点D,利用△ABO≌△CAD,求出点C的坐标,最后利用待定系数法求出AC的解析式.
(3)过点P作PE⊥x轴于点E,利用勾股定理即可求出AB=AC=2![]() ,利用S△APB=SOAB+S△OPB-S△OPA列出方程求出m的值.
,利用S△APB=SOAB+S△OPB-S△OPA列出方程求出m的值.
(1)令x=0代入y=-2x+4中
∴y=4,
∴B(0,4)
令y=0代入y=-2x+4中
∴x=2,
∴A(2,0)
(2)过点C作CD⊥x轴于点D,
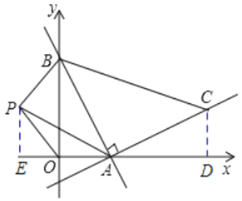
∵∠BAC=90°,
∴∠DAC+∠BAO=∠ABO+∠BAO=90°,
∴∠ABO=∠DAC,
在△ABO与△CAD中,
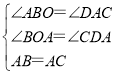
∴△ABO≌△CAD(AAS)
∴CD=OA=2,AD=OB=4,
∴OD=6,
∴C(6,2)
设直线AC的解析式为y=kx+b
∴![]()
∴解得: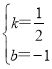
∴直线AC的解析式为:y=![]() x-1
x-1
(3)过点P作PE⊥x轴于点E,
∴PE=3,OE=-m
∵AB=AC=2![]()
∴S△ABC=![]() ACAB=
ACAB=![]() ×2
×2![]() ×2
×2![]() =10
=10
∴S△APB=SOAB+S△OPB-S△OPA
=![]() AOBO+
AOBO+![]() OBOE-
OBOE-![]() OAPE
OAPE
=1-2m
∴1-2m=10
∴m=-![]() .
.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD在直角坐标系中,边BC在x轴上,B点坐标为(m,0)且m>0.AB=a,BC=b,且满足b=![]() .
.
(1)求a,b的值及用m表示出点D的坐标;
(2)连接OA,AC,若△OAC为等腰三角形,求m的值;
(3)△OAC能为直角三角形吗?若能,求出m的值;若不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
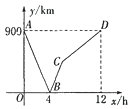
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km).图中的折线表示y与x之间的函数关系.根据图象进行以下探究:
(1)甲、乙两地之间的距离为_________km;
(2)求慢车和快车的速度;
(3)请解释图中点C的实际意义;
(4)分别写出线段AB、BC所表示的y与x之间的函数关系式;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是__________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下面的网格图中按要求画出图形,并回答问题:
(1)先画出△ABC向下平移5格后的△A1B1C1,再画出△ABC以点O为旋转中心,沿逆时针方向旋转90°后得到的△A2B2C2;
(2)如图,以点O为原点建立平面直角坐标系,试写出点A2,B1的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
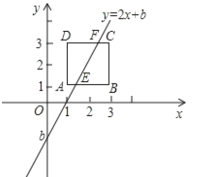
【题目】如图,已知正方形ABCD的顶点A(1,1),B(3,1),直线y=2x+b交边AB于点E,交边CD于点F,则直线y=2x+b 在y 轴上的截距b的变化范围是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEB中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是

A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com