
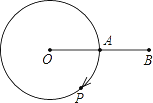
【题目】如图,A是半径为6cm的⊙O上的定点,动点P从A出发,以πcm/s的速度沿圆周按顺时针方向运动,当点P回到A时立即停止运动.设点P运动时间为t(s);
(1)当t=6s时,∠POA的度数是________;
(2)当t为多少时,∠POA=120°;
(3)如果点B是OA延长线上的一点,且AB=AO,问t为多少时,△POB为直角三角形?请说明理由.
【答案】(1)180;当点P运动的时间t为4s或8s时,∠POA=120°;(3)当点P运动的时间为2s或3s或9s或10s时,△POB为直角三角形.
【解析】
(1)先根据路程=速度×时间得出当t=6s时,点P运动的路程即弧AP的长度,再根据弧长公式即可求出∠POA的度数;
(2)当∠POA=120°时,点P运动的路程为⊙O周长的![]() 或
或![]() ,所以分两种情况进行分析;
,所以分两种情况进行分析;
(3)△POB为直角三角形时,由于动点P沿圆周运动,所以以B为顶点的角不可能为直角,那么分∠POB=90°,∠OPB=90°两种情况进行分析.
解:(1)设∠POA=n°,则
![]() =6π=
=6π=![]() ,
,
∴n=180.
即∠POA的度数是180.
故答案为180;
(2)当∠POA=120°时,如图,点P运动的路程为⊙O周长的![]() (图中P1处)或
(图中P1处)或![]() (图中P2处),
(图中P2处),
设点P运动的时间为ts.
当点P运动的路程为⊙O周长的![]() 时,πt=
时,πt=![]() 2π6,
2π6,
解得t=4;
当点P运动的路程为⊙O周长的![]() 时,πt=
时,πt=![]() 2π6,
2π6,
解得t=8;
∴当点P运动的时间t为4s或8s时,∠POA=120°;
(3)分两种情况:
①当∠POB=90°时,如图,点P运动的路程为⊙O周长的![]() (图中P1处)或
(图中P1处)或![]() (图中P2处),
(图中P2处),
设点P运动的时间为ts.
当点P运动的路程为⊙O周长的![]() 时,πt=
时,πt=![]() 2π6,
2π6,
解得t=3;
当点P运动的路程为⊙O周长的![]() 时,πt=
时,πt=![]() 2π6,
2π6,
解得t=9.
∴当点P运动的时间为3s或9s时,△POB为直角三角形;
②当∠OPB=90°时,如图,(图中P3处)或(图中P4处),
设点P运动的时间为ts.
当点P运动P3处时,连接AP3.
∵∠OP3B=90°,OA=AB,
∴AP3=OA=OP3,
∴△OAP3是等边三角形,
∴∠AOP3=60°,
∴πt=![]() 2π6,
2π6,
解得t=2;
当点P运动P4处时,连接AP4.
∵∠OP4B=90°,OA=AB,
∴AP4=OA=OP4,
∴△OAP4是等边三角形,
∴∠AOP4=60°,
∴πt=(1﹣![]() )2π6,
)2π6,
解得t=10.
∴当点P运动的时间为2s或10s时,△POB为直角三角形.
综上可知,当点P运动的时间为2s或3s或9s或10s时,△POB为直角三角形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
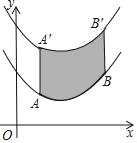
【题目】如图,将函数![]() 的图象沿y轴向上平移得到新函数图象,其中原函数图象上的两点A(1,m)、B(4,n)平移后对应新函数图象上的点分别为点A′、B′.若阴影部分的面积为6,则新函数的表达式为( )
的图象沿y轴向上平移得到新函数图象,其中原函数图象上的两点A(1,m)、B(4,n)平移后对应新函数图象上的点分别为点A′、B′.若阴影部分的面积为6,则新函数的表达式为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是甲、乙两个圆柱形水槽的轴截面示意图.乙槽中有一圆柱形铁块放在其中(圆柱形铁块的下底面完全落在水槽底面上),现将甲槽中的水匀速注人乙槽.甲、乙两个水槽中水的深度![]() 与注水时间
与注水时间![]() (分钟)之间的关系如图2所示.根据图象提供的信息,解答下列问题:
(分钟)之间的关系如图2所示.根据图象提供的信息,解答下列问题:
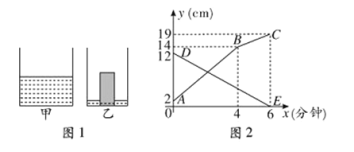
(1)图2中折线![]() 表示 槽中的水的深度与注水时间的关系,线段
表示 槽中的水的深度与注水时间的关系,线段![]() 表示 槽中的水的深度与注水时间的关系(填“甲”或“乙”),点
表示 槽中的水的深度与注水时间的关系(填“甲”或“乙”),点![]() 的纵坐标表示的实际意义是 ;
的纵坐标表示的实际意义是 ;
(2)当![]() 时,分别求出
时,分别求出![]() 和
和![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)注水多长时间时,甲、乙两个水槽中的水深度相同?
(4)若乙槽底面积为![]() 平方厘米(壁厚不计) ,求乙槽中铁块的体积.
平方厘米(壁厚不计) ,求乙槽中铁块的体积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题发现:
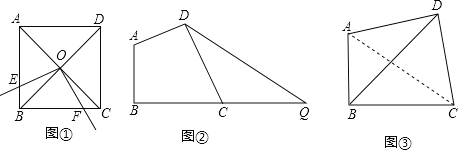
(1)如图①,正方形ABCD的边长为4,对角线AC、BD相交于点O,E是AB上点(点E不与A、B重合),将射线OE绕点O逆时针旋转90°,所得射线与BC交于点F,则四边形OEBF的面积为 .
问题探究:
(2)如图②,线段BQ=10,C为BQ上点,在BQ上方作四边形ABCD,使∠ABC=∠ADC=90°,且AD=CD,连接DQ,求DQ的最小值;
问题解决:
(3)“绿水青山就是金山银山”,某市在生态治理活动中新建了一处南山植物园,图③为南山植物园花卉展示区的部分平面示意图,在四边形ABCD中,∠ABC=∠ADC=90°,AD=CD,AC=600米.其中AB、BD、BC为观赏小路,设计人员考虑到为分散人流和便观赏,提出三条小路的长度和要取得最大,试求AB+BD+BC的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
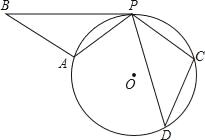
【题目】如图,已知△PDC是⊙O的内接三角形,CP=CD,若将△PCD绕点P顺时针旋转,当点C刚落在⊙O上的A处时,停止旋转,此时点D落在点B处.
(1)求证:PB与⊙O相切;
(2)当PD=2![]() ,∠DPC=30°时,求⊙O的半径长.
,∠DPC=30°时,求⊙O的半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小美周末去公园玩,发现公园一角有一种“守株待兔”的游戏,该游戏老板说明游戏规则如下:提供一只兔子和一个有A、B、C、D、E五个出口的兔笼,而且笼内的兔子从每个出口走出兔笼的机会是均等的,玩家只能将兔子从A、B两个出入口放兔子,如果兔子进笼子后从开始进入的入口出来,则玩家可获得价值5元的小兔玩具一只,否则,应付3元的参与费用.
(1)用作表或树状图列出小美参与游戏的所有可能结果,并求出小美得到玩具兔子的概率.
(2)假设有100人玩这个游戏,估计老板约赚多少钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题(不写作法,保留作图痕迹)
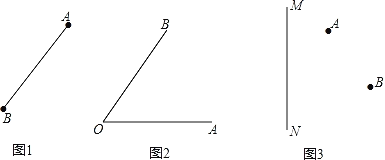
(1)如图1请利用直尺和圆规作线段AB的中垂线EF;
(2)如图2请利用直尺和圆规作∠AOB的角平分线OC;
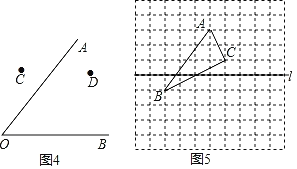
(3)如图3,要在公路MN上修一个车站P,使得P向AB两个地方的距离和最小,请利用直尺和圆规画出P的位置;
(4)如图4,已知∠AOB及点C、D两点,请利用直尺和圆规作一点P,使得点P到射线OA、OB的距离相等,且P点到点C、D的距离也相等;
(5)如图5,利用网状格画出△ABC关于直线l的对称图形△A'B'C'.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为发展学生的核心素养,培养学生的综合能力,某学校计划开设四门选修课:乐器、舞蹈、绘画、书法.学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).对调查结果进行整理,绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:
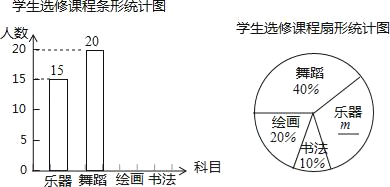
(1)本次调查的学生共有 人,在扇形统计图中,m的值是 ;
(2)将条形统计图补充完整;
(3)在被调查的学生中,选修书法的有2名女同学,其余为男同学,现要从中随机抽取2名同学代表学校参加某社区组织的书法活动,请写出所抽取的2名同学恰好是1名男同学和1名女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)如图,在建立了平面直角坐标系的正方形网格中,A(2,2),B(1,0),C(3,1)
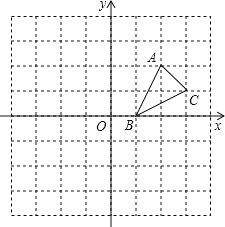
(1)画出ΔABC关于x轴对称的ΔA1B1C1.
(2)画出将ΔABC绕点B逆时针旋转900,所得的ΔA2B2C2.
(3)直接写出A2点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com