
【题目】作图题(不写作法,保留作图痕迹)
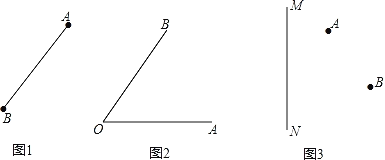
(1)如图1请利用直尺和圆规作线段AB的中垂线EF;
(2)如图2请利用直尺和圆规作∠AOB的角平分线OC;
(3)如图3,要在公路MN上修一个车站P,使得P向AB两个地方的距离和最小,请利用直尺和圆规画出P的位置;
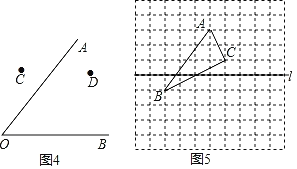
(4)如图4,已知∠AOB及点C、D两点,请利用直尺和圆规作一点P,使得点P到射线OA、OB的距离相等,且P点到点C、D的距离也相等;
(5)如图5,利用网状格画出△ABC关于直线l的对称图形△A'B'C'.
【答案】(1)如图1,直线EF为所作;见解析;(2)如图2,射线OC为所作;见解析;(3)如图3,点P为所作;见解析;(4)如图4,点P为所作;见解析;(5)如图5,△A′B′C′为所作.见解析.
【解析】
(1)利用基本作图,作线段AB的垂直平分线得到直线EF;
(2)利用基本作图,作OC平分;
(3)作A点关于MN的对称点A′,连接BA′交MN于P,利用两点之间线段最短可判断P点满足条件;
(4)作线段CD的垂直平分线和∠AOB的平分线,它们相交于点P,则点P满足条件;
(5)利用网格特点和对称的性质分别画出A、B、C的对称点A′、B′、C′即可.
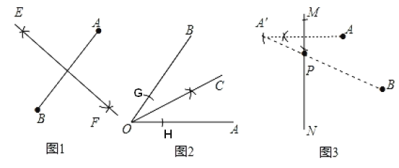
(1)如图1,分别以点A和点B为圆心,以任意长为半径画弧,两弧相较于E、F两点,连接E、F两点,直线EF为所作;
(2)如图2,以点O为圆心,任意长为半径画弧,交∠AOB于两点G、H,再以两交点为圆心,大于![]() GH的长为半径画弧,两弧交于一点C,连接OC,射线OC为所作;
GH的长为半径画弧,两弧交于一点C,连接OC,射线OC为所作;
(3)如图3,作A点关于MN的对称点A′,连接BA′交MN于P,点P为所作;
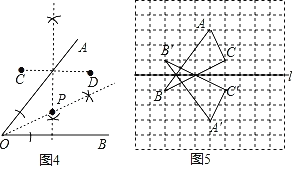
(4)如图4,作线段CD的垂直平分线和∠AOB的平分线,它们相交于点P,点P为所作;
(5)如图5,利用网格特点和对称的性质分别画出A、B、C的对称点A′、B′、C′,顺次连接点A′、B′、C′,△A′B′C′为所作.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
【题目】列方程或方程组解应用题:
为了响应“十三五”规划中提出的绿色环保的倡议,某校文印室提出了每个人都践行“双面打印,节约用纸”.已知打印一份资料,如果用A4厚型纸单面打印,总质量为400克,将其全部改成双面打印,用纸将减少一半;如果用A4薄型纸双面打印,这份资料的总质量为160克,已知每页薄型纸比厚型纸轻0.8克,求A4薄型纸每页的质量.(墨的质量忽略不计)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平行四边形ABCD中,AB=5,BC=8,cosB=![]() ,点E是BC边上的动点,当以CE为半径的⊙C与边AD有两个交点时,半径CE的取值范围是( )
,点E是BC边上的动点,当以CE为半径的⊙C与边AD有两个交点时,半径CE的取值范围是( )
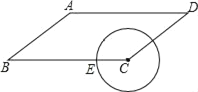
A. 0<CE≤8 B. 0<CE≤5 C. 3<CE≤8 D. 3<CE≤5
查看答案和解析>>
科目:初中数学 来源: 题型:
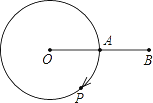
【题目】如图,A是半径为6cm的⊙O上的定点,动点P从A出发,以πcm/s的速度沿圆周按顺时针方向运动,当点P回到A时立即停止运动.设点P运动时间为t(s);
(1)当t=6s时,∠POA的度数是________;
(2)当t为多少时,∠POA=120°;
(3)如果点B是OA延长线上的一点,且AB=AO,问t为多少时,△POB为直角三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
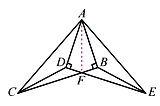
【题目】如图,已知Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,BC与DE相交于点F,连接CD,EB.
(1)图中还有几对全等三角形,请你一一列举;
(2)求证:CF=EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
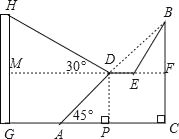
【题目】为邓小平诞辰110周年献礼,广安市政府对城市建设进行了整改,如图,已知斜坡AB长60![]() 米,坡角(即∠BAC)为45°,BC⊥AC,现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE(下面两个小题结果都保留根号).
米,坡角(即∠BAC)为45°,BC⊥AC,现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE(下面两个小题结果都保留根号).
(1)若修建的斜坡BE的坡比为![]() :1,求休闲平台DE的长是多少米?
:1,求休闲平台DE的长是多少米?
(2)一座建筑物GH距离A点33米远(即AG=33米),小亮在D点测得建筑物顶部H的仰角(即∠HDM)为30°.点B、C、A、G,H在同一个平面内,点C、A、G在同一条直线上,且HG⊥CG,问建筑物GH高为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
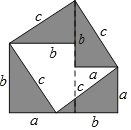
【题目】(1)勾股定理的证法多样,其中“面积法”是常用方法,小明发现:当四个全等的直角三角形如图摆放时,可以用“面积法”来证明勾股定理.(写出勾股定理的内容并证明)
(2)已知实数x,y,z满足:![]() ,试问长度分别为x、y、z的三条线段能否组成一个三角形?如果能,请求出该三角形的面积;如果不能,请说明理由.
,试问长度分别为x、y、z的三条线段能否组成一个三角形?如果能,请求出该三角形的面积;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
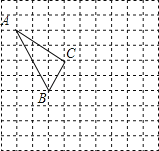
【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(﹣4,5),(﹣1,3).
(1)在如图所示的网格平面内作出平面直角坐标系,标注原点以及x轴、y轴;
(2)作出△ABC关于y轴对称的△A′B′C′,并写出点B′的坐标;
(3)点P是x轴上的动点,在图中找出使△A′BP周长最小时的点P,直接写出点P的坐标是: .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com