
【题目】已知k为实数,关于x的方程为x2﹣2(k+1)x+k2=0.
(1)请判断x=﹣1是否可为此方程的根,说明理由.
(2)设方程的两实根为x1,x2,当2x1+2x2+1=x1x2时,试求k的值.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某校组织了一次环保知识竞赛,每班选25名同学参加比赛,成绩分别为A、B、C、D四个等级,其中相应等级的得分依次记为100分、90分、80分、70分,学校将某年级的一班和二班的成绩整理并绘制成统计图,试根据以上提供的信息解答下列问题:
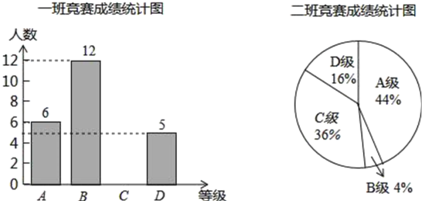
(1)把一班竞赛成绩统计图补充完整;
(2)根据下表填空:a= ,b= ,c= ;
平均数(分) | 中位数(分) | 众数(分) | |
一班 | a | b | 90 |
二班 | 87.6 | 80 | c |
(3)请从平均数和中位数或众数中任选两个对这次竞赛成绩的结果进行分析.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】凯里市某文具店某种型号的计算器每只进价12元,售价20元,多买优惠,优势方法是:凡是一次买10只以上的,每多买一只,所买的全部计算器每只就降价0.1元,例如:某人买18只计算器,于是每只降价0.1×(18﹣10)=0.8(元),因此所买的18只计算器都按每只19.2元的价格购买,但是每只计算器的最低售价为16元.
(1)求一次至少购买多少只计算器,才能以最低价购买?
(2)求写出该文具店一次销售x(x>10)只时,所获利润y(元)与x(只)之间的函数关系式,并写出自变量x的取值范围;
(3)一天,甲顾客购买了46只,乙顾客购买了50只,店主发现卖46只赚的钱反而比卖50只赚的钱多,请你说明发生这一现象的原因;当10<x≤50时,为了获得最大利润,店家一次应卖多少只?这时的售价是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函y=kx+b的图象经过点A(-2,4),且与正比例函数![]() 的图象交于点B(a,2).
的图象交于点B(a,2).
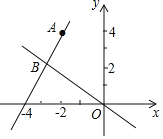
(1)求a的值及一次函数y=kx+b的解析式;
(2)若一次函数y=kx+b的图象与x轴交于点C,且正比例函数y=-![]() x的图象向下平移m(m>0)个单位长度后经过点C,求m的值;
x的图象向下平移m(m>0)个单位长度后经过点C,求m的值;
(3)直接写出关于x的不等式0<![]() <kx+b的解集.
<kx+b的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某部队将在指定山区进行军事演习,为了使道路便于部队重型车辆通过,部队工兵连接到抢修一段长3600米道路的任务,按原计划完成总任务的![]() 后,为了让道路尽快投入使用,工兵连将工作效率提高了50%,一共用了10小时完成任务.
后,为了让道路尽快投入使用,工兵连将工作效率提高了50%,一共用了10小时完成任务.
(1)按原计划完成总任务的![]() 时,已抢修道路 米;
时,已抢修道路 米;
(2)求原计划每小时抢修道路多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将函数![]() 的图象沿y轴向上平移得到新函数图象,其中原函数图象上的两点A(1,m)、B(4,n)平移后对应新函数图象上的点分别为点A′、B′.若阴影部分的面积为6,则新函数的表达式为( )
的图象沿y轴向上平移得到新函数图象,其中原函数图象上的两点A(1,m)、B(4,n)平移后对应新函数图象上的点分别为点A′、B′.若阴影部分的面积为6,则新函数的表达式为( )
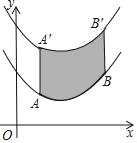
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校开展“书香校园”活动以来,受到同学们的广泛关注,学位为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制成如下不完整的统计图表.
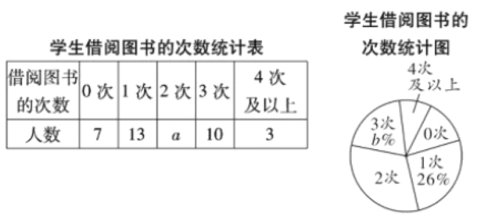
请你根据统计图表中的信息,解答下列问题:
(1)![]() =___________,
=___________,![]() =_____________;
=_____________;
(2)该调查统计数据的中位数是_________,众数是__________;
(3)请计算扇形统计图中“3次”所对应扇形的圆心角的度数;
(4)若该校共有2000名学生,根据调查结果,估计该校学生在一周内借阅图书“4次及以上”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题发现:
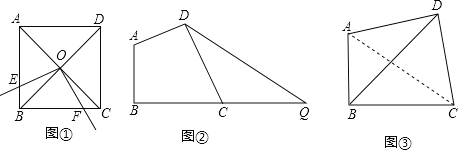
(1)如图①,正方形ABCD的边长为4,对角线AC、BD相交于点O,E是AB上点(点E不与A、B重合),将射线OE绕点O逆时针旋转90°,所得射线与BC交于点F,则四边形OEBF的面积为 .
问题探究:
(2)如图②,线段BQ=10,C为BQ上点,在BQ上方作四边形ABCD,使∠ABC=∠ADC=90°,且AD=CD,连接DQ,求DQ的最小值;
问题解决:
(3)“绿水青山就是金山银山”,某市在生态治理活动中新建了一处南山植物园,图③为南山植物园花卉展示区的部分平面示意图,在四边形ABCD中,∠ABC=∠ADC=90°,AD=CD,AC=600米.其中AB、BD、BC为观赏小路,设计人员考虑到为分散人流和便观赏,提出三条小路的长度和要取得最大,试求AB+BD+BC的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com