
【题目】如图,在平面直角坐标系xOy中,一次函y=kx+b的图象经过点A(-2,4),且与正比例函数![]() 的图象交于点B(a,2).
的图象交于点B(a,2).
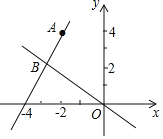
(1)求a的值及一次函数y=kx+b的解析式;
(2)若一次函数y=kx+b的图象与x轴交于点C,且正比例函数y=-![]() x的图象向下平移m(m>0)个单位长度后经过点C,求m的值;
x的图象向下平移m(m>0)个单位长度后经过点C,求m的值;
(3)直接写出关于x的不等式0<![]() <kx+b的解集.
<kx+b的解集.
【答案】(1)y=2x+8;(2)m=![]() ;(3)-3<x<0
;(3)-3<x<0
【解析】
(1)先确定B的坐标,然后根据待定系数法求解析式;
(2)先求得C的坐标,然后根据题意求得平移后的直线的解析式,把C的坐标代入平移后的直线的解析式,即可求得M的值;
(3)找出直线y=-![]() x落在y=kx+b的下方且在x轴上方的部分对应的x的取值范围即可.
x落在y=kx+b的下方且在x轴上方的部分对应的x的取值范围即可.
解:(1)∵正比例函数![]() 的图象经过点B(a,2),
的图象经过点B(a,2),
∴2=-![]() a,解得,a=-3,
a,解得,a=-3,
∴B(-3,2),
∵一次函数y=kx+b的图象经过点A(-2,4),B(-3,2),
∴![]() ,解得
,解得![]() ,
,
∴一次函数y=kx+b的解析式为y=2x+8;
(2)∵一次函数y=2x+8的图象与x轴交于点C,
∴C(-4,0),
∵正比例函数y=-![]() x的图象向下平移m(m>0)个单位长度后经过点C,
x的图象向下平移m(m>0)个单位长度后经过点C,
∴平移后的函数的解析式为y=-![]() x-m,
x-m,
∴0=-![]() ×(-4)-m,
×(-4)-m,
解得m=![]() ;
;
(3)∵一次函y=kx+b与正比例函数y=-![]() x的图象交于点B(-3,2),
x的图象交于点B(-3,2),
且一次函数y=2x+8的图象与x轴交于点C(-4,0),
∴关于x的不等式0<-![]() x<kx+b的解集是-3<x<0.
x<kx+b的解集是-3<x<0.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
【题目】如图所示,某工程队准备在山坡(山坡视为直线l)上修一条路,需要测量山坡的坡度,即tanα的值.测量员在山坡P处(不计此人身高)观察对面山顶上的一座铁塔,测得塔尖C的仰角为31°,塔底B的仰角为26.6°.已知塔高BC=40米,塔所在的山高OB=240米,OA=300米,图中的点O、B、C、A、P在同一平面内.
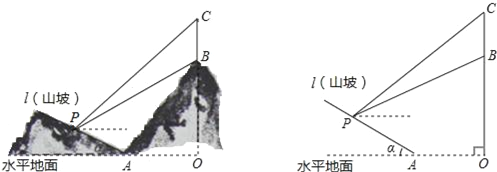
求:
(1)P到OC的距离.
(2)山坡的坡度tanα.
(参考数据sin26.6°≈0.45,tan26.6°≈0.50;sin31°≈0.52,tan31°≈0.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,D在边AC上,且
,D在边AC上,且![]() .
.
![]() 如图1,填空
如图1,填空![]() ______
______![]() ,
,![]() ______
______![]()
![]() 如图2,若M为线段AC上的点,过M作直线
如图2,若M为线段AC上的点,过M作直线![]() 于H,分别交直线AB、BC与点N、E.
于H,分别交直线AB、BC与点N、E.
![]() 求证:
求证:![]() 是等腰三角形;
是等腰三角形;
![]() 试写出线段AN、CE、CD之间的数量关系,并加以证明.
试写出线段AN、CE、CD之间的数量关系,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核.甲、乙、丙各项得分如下表:
笔 试 | 面 试 | 体 能 | |
甲 | 85 | 80 | 75 |
乙 | 80 | 90 | 73 |
丙 | 83 | 79 | 90 |
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序.
(2)该公司规定:笔试,面试、体能得分分别不得低于80分,80分,70分,并按60%,30%,10%的比例计入总分(不计其他因素条件),请你说明谁将被录用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,∠ABC=60°,BD平分∠ADC.
(1)试说明△ABC是等边三角形;
(2)若AD=2,DC=4,求四边形ABCD的面积.
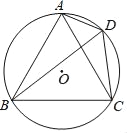
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知k为实数,关于x的方程为x2﹣2(k+1)x+k2=0.
(1)请判断x=﹣1是否可为此方程的根,说明理由.
(2)设方程的两实根为x1,x2,当2x1+2x2+1=x1x2时,试求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
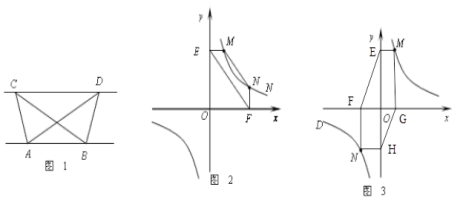
【题目】(1)探究新知:如图1,已知△ABC与△ABD的面积相等, 试判断AB与CD的位置关系,并说明理由.
(2)结论应用:如图2,点M,N在反比例函数![]() (k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F. 试证明:MN∥EF.
(k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F. 试证明:MN∥EF.
(3)变式探究:如图3,点M,N在反比例函数![]() (k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,过点M作MG⊥x轴,过点N作NH⊥y轴,垂足分别为E、F、G、H. 试证明:EF ∥GH.
(k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,过点M作MG⊥x轴,过点N作NH⊥y轴,垂足分别为E、F、G、H. 试证明:EF ∥GH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程或方程组解应用题:
为了响应“十三五”规划中提出的绿色环保的倡议,某校文印室提出了每个人都践行“双面打印,节约用纸”.已知打印一份资料,如果用A4厚型纸单面打印,总质量为400克,将其全部改成双面打印,用纸将减少一半;如果用A4薄型纸双面打印,这份资料的总质量为160克,已知每页薄型纸比厚型纸轻0.8克,求A4薄型纸每页的质量.(墨的质量忽略不计)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平行四边形ABCD中,AB=5,BC=8,cosB=![]() ,点E是BC边上的动点,当以CE为半径的⊙C与边AD有两个交点时,半径CE的取值范围是( )
,点E是BC边上的动点,当以CE为半径的⊙C与边AD有两个交点时,半径CE的取值范围是( )
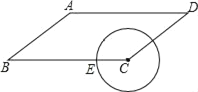
A. 0<CE≤8 B. 0<CE≤5 C. 3<CE≤8 D. 3<CE≤5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com