【题目】张大伯计划建一个面积为72平方米的矩形养鸡场，为了节约材料，鸡场一边靠着原有的一堵墙（墙长15米），另外的部分（包括中间的隔墙）用30米的竹篱笆围成，如图．
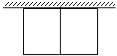
（1）请你通过计算帮助张大伯设计出围养鸡场的方案．
（2）在上述条件不变的情况下，能围出比72平方米更大的养鸡场吗？请说明理由．
口算题卡加应用题集训系列答案
综合自测系列答案科目：初中数学 来源： 题型：
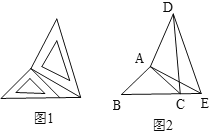
【题目】两个大小不同的等腰直角三角尺如图1所示放置，图2是由它抽象出的几何图形，点
，
，
在同一条直线上，连接
．
（1）请找出图2中与
全等的三角形，并说明理由(说明：结论中不得含有未标识的字母)；
（2）判断线段与
是否垂直，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，函数y1=－x+4的图象与函数y2=
(x＞0)的图象交于 A(a，1)、B(1，b)两点.
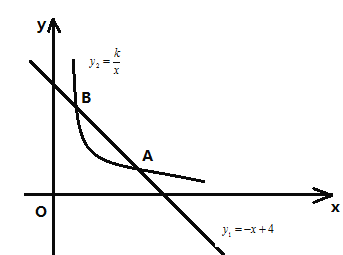
(1)求a，b及y2的函数关系式；
(2)观察图象，当x＞0时，比较y1与y2大小.
查看答案和解析>>
科目：初中数学 来源： 题型：
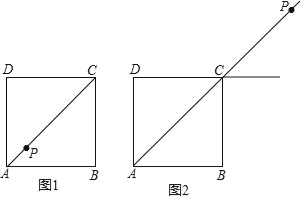
【题目】在正方形ABCD中，点P在射线AC上，作点P关于直线CD的对称点Q，作射线BQ交射线DC于点E，连接BP．
（1）当点P在线段AC上时，如图1．
①依题意补全图1；
②若EQ=BP，则∠PBE的度数为 ，并证明；
（2）当点P在线段AC的延长线上时，如图2．若EQ=BP，正方形ABCD的边长为1，请写出求BE长的思路．（可以不写出计算结果）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】河南省旅游资源丰富，2013～2017年旅游收入不断增长，同比增速分别为：15.3%，12.7%，15.3%，14.5%，17.1%．关于这组数据，下列说法正确的是（ ）
A. 中位数是12.7% B. 众数是15.3%
C. 平均数是15.98% D. 方差是0
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线AB、CD相交于点O，∠AOC=30°，⊙P的半径为1cm，且OP=6cm，如果⊙P以1cm/s的速度沿由A向B的方向移动，那么多少秒后⊙P与直线CD相切（ ）
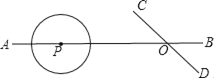
A. 4或8 B. 4或6 C. 8 D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，AD是BC边上的中线，AE是BC边上的高．
（1）若∠ACB＝100°，求∠CAE的度数；
（2）若S△ABC＝12，CD＝4，求高AE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线与x轴的交点坐标分别为A（1，0），B（x2，0）（点B在点A的右侧），其对称轴是x=3，该函数有最小值是﹣2．
（1）求二次函数解析式；
（2）在图1上作平行于x轴的直线，交抛物线于C（x3，y3），D（x4，y4），求x3+x4的值；
（3）将（1）中函数的部分图象（x＞x2）向下翻折与原图象未翻折的部分组成图象“G”，如图2，在（2）中平行于x轴的直线取点E（x5，y5）、（x4＜x5），结合函数图象求x3+x4+x5的取值范围．
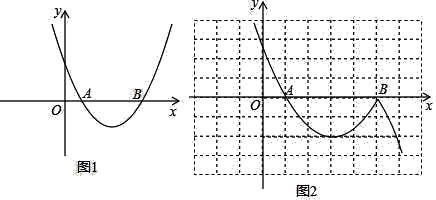
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义：如果两条线段将一个三角形分成3个小等腰三角形，我们把这两条线段叫做这个三角形的三分线．
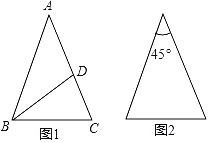
（1）如图1，在△ABC中，AB＝AC，点D在AC边上，且AD＝BD＝BC，求∠A的大小；
（2）在图1中过点C作一条线段CE，使BD，CE是△ABC的三分线；在图2中画出顶角为45°的等腰三角形的三分线，并标注每个等腰三角形顶角的度数；
（3）在△ABC中，∠B＝30°，AD和DE是△ABC的三分线，点D在BC边上，点E在AC边上，且AD＝BD，DE＝CE，请直接写出∠C所有可能的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
