
【题目】如图,函数y1=-x+4的图象与函数y2=![]() (x>0)的图象交于 A(a,1)、B(1,b)两点.
(x>0)的图象交于 A(a,1)、B(1,b)两点.
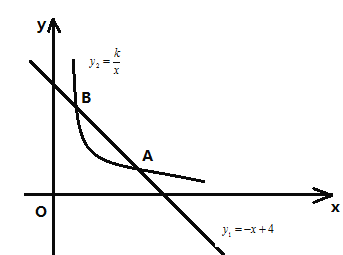
(1)求a,b及y2的函数关系式;
(2)观察图象,当x>0时,比较y1与y2大小.
科目:初中数学 来源: 题型:
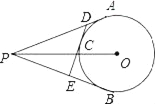
【题目】如图,PA、PB切⊙O于A、B,点C在弧AB上,DE切⊙O于C,交PA、PB于D、E,已知PO=13cm,⊙O的半径为5cm,则△PDE的周长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
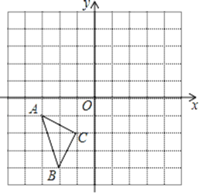
【题目】在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(﹣3,﹣1).
(1)将△ABC沿y轴正方向平移3个单位得到△A1B1C1,画出△A1B1C1,并写出点B1的坐标;
(2)画出△A1B1C1关于y轴对称的△A2B2C2,并写出点C2的坐标;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
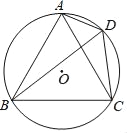
【题目】如图,四边形ABCD内接于⊙O,∠ABC=60°,BD平分∠ADC.
(1)试说明△ABC是等边三角形;
(2)若AD=2,DC=4,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
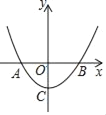
【题目】如图,二次函数y=x2﹣m2(m>0且为常数)的图象与x轴交于点A、B(A在B左侧),与y轴交于C.
(1)求A,B,C三点的坐标(用含m的式子表示);
(2)若∠ACB=90°,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
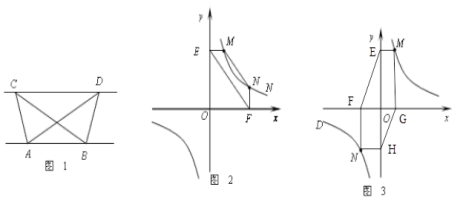
【题目】(1)探究新知:如图1,已知△ABC与△ABD的面积相等, 试判断AB与CD的位置关系,并说明理由.
(2)结论应用:如图2,点M,N在反比例函数![]() (k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F. 试证明:MN∥EF.
(k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F. 试证明:MN∥EF.
(3)变式探究:如图3,点M,N在反比例函数![]() (k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,过点M作MG⊥x轴,过点N作NH⊥y轴,垂足分别为E、F、G、H. 试证明:EF ∥GH.
(k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,过点M作MG⊥x轴,过点N作NH⊥y轴,垂足分别为E、F、G、H. 试证明:EF ∥GH.
查看答案和解析>>
科目:初中数学 来源: 题型:
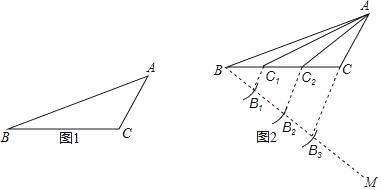
【题目】石景山区八角北路有一块三角形空地(如图1)准备绿化,拟从点A出发,将△ABC分成面积相等的三个三角形,栽种三种不同的花草.
下面是小美的设计(如图2).
作法:(1)作射线BM;
(2)在射线BM上顺次截取BB1=B1B2=B2B3;
(3)连接B3C,分别过B1、B2作B1C1∥B2C2∥B3C,交BC于点C1、C2;
(4)连接AC1、AC2.则![]() .
.
请回答,![]() 成立的理由是:
成立的理由是:
①_____;
②_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张大伯计划建一个面积为72平方米的矩形养鸡场,为了节约材料,鸡场一边靠着原有的一堵墙(墙长15米),另外的部分(包括中间的隔墙)用30米的竹篱笆围成,如图.
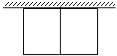
(1)请你通过计算帮助张大伯设计出围养鸡场的方案.
(2)在上述条件不变的情况下,能围出比72平方米更大的养鸡场吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
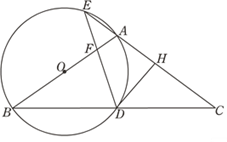
【题目】如图,在△ABC中,AB=AC,以AB为直径作圆O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.
(1)求证:DH是圆O的切线;
(2)若![]() ,求证:A为EH的中点.
,求证:A为EH的中点.
(3)若EA=EF=1,求圆O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com