
【题目】观察分析下列方程:
①![]() 的解是
的解是![]() 或
或![]() ;
;
②![]() 的解是
的解是![]() 或
或![]() ;
;
③![]() 的解是
的解是![]() 或
或![]() ;
;
……
利用它们所蕴含的规律,则关于![]() 的方程
的方程![]() (
(![]() 为正整数)的解是_____.
为正整数)的解是_____.
【答案】x=n+3或x=n+4
【解析】
根据已知三个分式方程和分式方程的解可得出规律:方程左边分式的分母是方程的解的乘积,方程右边是方程的解的和,把x-3看成一个整体,根据规律即可得答案.
①中,方程的解为x=1或x=2,1×2=2,1+2=3,
②中,方程的解为x=2或x=3,2×3=6,2+3=5,
③中,方程的解为x=3或x=4,3×4=12,3+4=7,
……
∴关于x的方程x+![]() =2a+1(a为正整数)的解为x=a或x=a+1,
=2a+1(a为正整数)的解为x=a或x=a+1,
把![]() 变形得:
变形得:![]() ,
,
∴x-3=n或x-3=n+1,
∴x=n+3或x=n+4,
∴关于![]() 的方程
的方程![]() (
(![]() 为正整数)的解是x=n+3或x=n+4,
为正整数)的解是x=n+3或x=n+4,
故答案为:x=n+3或x=n+4


科目:初中数学 来源: 题型:
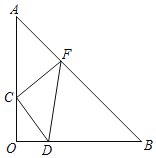
【题目】如图,△AOB中,∠AOB=90°,OA=OB,等腰直角△CDF的直角顶点C在边OA上,点D在边OB上,点F在边AB上,如果△CDF的面积是△AOB的面积的![]() ,OD=2,则△AOB的面积为____.
,OD=2,则△AOB的面积为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某工程队准备在山坡(山坡视为直线l)上修一条路,需要测量山坡的坡度,即tanα的值.测量员在山坡P处(不计此人身高)观察对面山顶上的一座铁塔,测得塔尖C的仰角为31°,塔底B的仰角为26.6°.已知塔高BC=40米,塔所在的山高OB=240米,OA=300米,图中的点O、B、C、A、P在同一平面内.
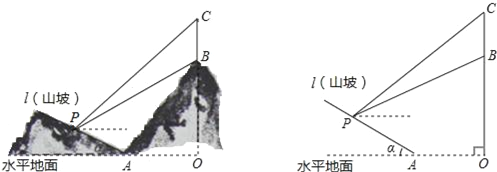
求:
(1)P到OC的距离.
(2)山坡的坡度tanα.
(参考数据sin26.6°≈0.45,tan26.6°≈0.50;sin31°≈0.52,tan31°≈0.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,以
,以![]() 的一边为边画等腰三角形,使得它的第三个顶点在
的一边为边画等腰三角形,使得它的第三个顶点在![]() 的其他边上,则可以画出的不同的等腰三角形的个数最多可画几个?( )
的其他边上,则可以画出的不同的等腰三角形的个数最多可画几个?( )
A.9个B.7个C.6个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古埃及人用下面的方法得到直角三角形,把一根长绳打上等距离的13个结(12段),然后用桩钉钉成一个三角形,如图1,其中∠C便是直角.
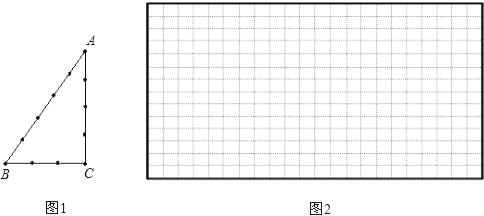
(1)请你选择古埃及人得到直角三角形这种方法的理由 (填A或B)
A.勾股定理:在直角三角形边的两直角边的平方和等于斜边的平方
B.勾股定理逆定理:如果三角形的三边长a、b、c有关系:a2+b2=c2,那么这个三角形是直角三角形
(2)如果三个正整数a、b、c满足a2+b2=c2,那么我们就称 a、b、c是一组勾股数,请你写出一组勾股数
(3)仿照上面的方法,再结合上面你写出的勾股数,你能否只用绳子,设计一种不同于上面的方法得到一个直角三角形(在图2中,只需画出示意图.)
查看答案和解析>>
科目:初中数学 来源: 题型:
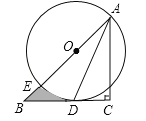
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E.
(1)求证:AD平分∠BAC;
(2)若CD=1,求图中阴影部分的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,D在边AC上,且
,D在边AC上,且![]() .
.
![]() 如图1,填空
如图1,填空![]() ______
______![]() ,
,![]() ______
______![]()
![]() 如图2,若M为线段AC上的点,过M作直线
如图2,若M为线段AC上的点,过M作直线![]() 于H,分别交直线AB、BC与点N、E.
于H,分别交直线AB、BC与点N、E.
![]() 求证:
求证:![]() 是等腰三角形;
是等腰三角形;
![]() 试写出线段AN、CE、CD之间的数量关系,并加以证明.
试写出线段AN、CE、CD之间的数量关系,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核.甲、乙、丙各项得分如下表:
笔 试 | 面 试 | 体 能 | |
甲 | 85 | 80 | 75 |
乙 | 80 | 90 | 73 |
丙 | 83 | 79 | 90 |
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序.
(2)该公司规定:笔试,面试、体能得分分别不得低于80分,80分,70分,并按60%,30%,10%的比例计入总分(不计其他因素条件),请你说明谁将被录用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程或方程组解应用题:
为了响应“十三五”规划中提出的绿色环保的倡议,某校文印室提出了每个人都践行“双面打印,节约用纸”.已知打印一份资料,如果用A4厚型纸单面打印,总质量为400克,将其全部改成双面打印,用纸将减少一半;如果用A4薄型纸双面打印,这份资料的总质量为160克,已知每页薄型纸比厚型纸轻0.8克,求A4薄型纸每页的质量.(墨的质量忽略不计)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com