
【题目】如图山坡上有一根旗杆AB,旗杆底部B点到山脚C点的距离BC为![]() 米,斜坡BC的坡度i=1:
米,斜坡BC的坡度i=1: ![]() .小明在山脚的平地F处测量旗杆的高,点C到测角仪EF的水平距离CF=1米,从E处测得旗杆顶部A的仰角为45°,旗杆底部B的仰角为20°.
.小明在山脚的平地F处测量旗杆的高,点C到测角仪EF的水平距离CF=1米,从E处测得旗杆顶部A的仰角为45°,旗杆底部B的仰角为20°.
(1)求坡角∠BCD;
(2)求旗杆AB的高度.
(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)

【答案】旗杆AB的高度为6.4米.
【解析】分析:(1)根据坡度i与坡角α之间的关系为:i=tanα进行计算;
(2)根据余弦的概念求出CD,根据正切的概念求出AG、BG,计算即可.
本题解析:(1)∵斜坡BC的坡度i=1: ![]() ,∴tan∠BCD=
,∴tan∠BCD= ![]() ,
,
∴∠BCD=30°;
(2)在Rt△BCD中,CD=BC×cos∠BCD=6![]() ×
×![]() =9,
=9,
则DF=DC+CF=10(米),∵四边形GDFE为矩形,∴GE=DF=10(米),
∵∠AEG=45°,∴AG=DE=10(米),
在Rt△BEG中,BG=GE×tan∠BEG=10×0.36=3.6(米),
则AB=AGBG=103.6=6.4(米).
答:旗杆AB的高度为6.4米。


 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】下列关于三角形的内心说法正确的是( )
A.内心是三角形三条角平分线的交点
B.内心是三角形三边中垂线的交点
C.内心到三角形三个顶点的距离相等
D.钝角三角形的内心在三角形外
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=6,AC=BC=5,将△ABC绕点A按顺时针方向旋转,得到△ADE,旋转角为α(0°<α<180°),点B的对应点为点D,点C的对应点为点E,连接BD,BE.
(1)如图,当α=60°时,延长BE交AD于点F.
①求证:△ABD是等边三角形;
②求证:BF⊥AD,AF=DF;
③请直接写出BE的长;
(2)在旋转过程中,过点D作DG垂直于直线AB,垂足为点G,连接CE,当∠DAG=∠ACB,且线段DG与线段AE无公共点时,请直接写出BE+CE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
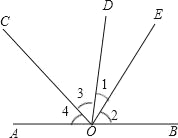
【题目】如图,已知O为直线AB上一点,过点O向直线AB上方引三条射线OC、OD、OE,且OC平分∠AOD,∠BOE=3∠DOE,∠COE=70°.
求:(1)∠BOE的度数;(2)∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B、C为数轴上的三点,动点A、B同时从原点出发,动点A每秒运动x个单位,动点B每秒运动y个单位,且动点A运动到的位置对应的数记为a,动点B运动到的位置对应的数记为b,定点C对应的数为8.
(1)若2秒后,a、b满足|a+8|+(b﹣2)2=0,则x= ,y= ,并请在数轴上标出A、B两点的位置.
(2)若动点A、B在(1)运动后的位置上保持原来的速度,且同时向正方向运动z秒后使得|a|=|b|,使得z= .
(3)若动点A、B在(1)运动后的位置上都以每秒2个单位向正方向运动继续运动t秒,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC,点A与点B之间的距离为AB,且AC+BC=1.5AB,则t= .
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,点E为BC边的中点,把△ABE沿直线AE折叠,B点落在点B′处,B′B与AE交于点F,连接AB′,DB′,FC.下列结论:①AB′=AD;②△FCB′为等腰直角三角形;③∠CB′D=135°;④BB′=BC;⑤![]() .其中正确的个数为( ).
.其中正确的个数为( ).
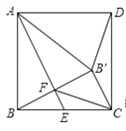
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com