
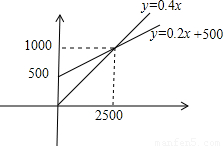
 解:(1)甲厂:y=0.2x+500,
解:(1)甲厂:y=0.2x+500,

 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
 (2004•聊城模拟)为了测得聊城铁塔的高度,小明在离铁塔10米处的点C测得塔顶A的仰角为α,小亮在离铁塔25米处的点D测得塔顶A的仰角为β(如图),恰巧α+β=90度.小明和小亮很快求出了铁塔AB的高度.你知道他俩是怎样求出来的吗?请写出你的解题过程(结果精确到0.01米).
(2004•聊城模拟)为了测得聊城铁塔的高度,小明在离铁塔10米处的点C测得塔顶A的仰角为α,小亮在离铁塔25米处的点D测得塔顶A的仰角为β(如图),恰巧α+β=90度.小明和小亮很快求出了铁塔AB的高度.你知道他俩是怎样求出来的吗?请写出你的解题过程(结果精确到0.01米).查看答案和解析>>
科目:初中数学 来源:2004年全国中考数学试题汇编《二次函数》(05)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2004年山东省聊城市中考数学试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2004年全国中考数学试题汇编《圆》(06)(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com