
【题目】如图,射线OA的方向是北偏东15°,射线OB的方向是北偏西40°,OA是∠BOC的平分线,射线OD是OB的反向延长线.

(1)射线OD的方向是
(2)在图中画出表示南偏东75°的射线OE;
(3)在(2)的条件下,求∠COE的度数
【答案】(1)南偏东40°;(2)作图见详解;(3)55°.
【解析】
(1)射线OD是OB的反向延长线,根据射线OB的方向即可判断射线OD的方向;
(2)用量角器在图中画出表示南偏东75°的射线OE即可;
(3)先求出∠COD,再减去∠DOE,即可求∠COE的度数.
解:(1) 由射线OB的方向是北偏西40°,OA是∠BOC的平分线,射线OD是OB的反向延长线,可得射线OD的方向是南偏东40°;
(2)作图如下:
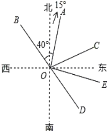
(3) 由题意可知OA是∠BOC的平分线,则有∠A0C=∠AOB=45°,∠COD=180°-∠A0C-∠AOB=90°,再由南偏东75°的射线OE,可知∠EOD=75°-40°=35°,可得∠COE=∠COD-∠EOD=90°-35°=55°.


科目:初中数学 来源: 题型:
【题目】某农科所对甲、乙两种小麦各选用10块面积相同的试验田进行种植试验,它们的平均亩产量分别是![]() =610千克,
=610千克, ![]() =609千克,亩产量的方差分别是
=609千克,亩产量的方差分别是![]() =29.6,
=29.6, ![]() =2.则关于两种小麦推广种植的合理决策是( )
=2.则关于两种小麦推广种植的合理决策是( )
A. 甲的平均亩产量较高,应推广甲
B. 甲、乙的平均亩产量相差不多,均可推广
C. 甲的平均亩产量较高,且亩产量比较稳定,应推广甲
D. 甲、乙的平均亩产量相差不多,但乙的亩产量比较稳定,应推广乙
查看答案和解析>>
科目:初中数学 来源: 题型:
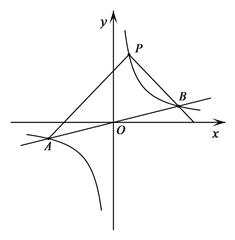
【题目】如图,反比例函数y=![]() 的图象与一次函数y=
的图象与一次函数y=![]() x的图象交于点A、B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.
x的图象交于点A、B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.
(1)若点P的坐标是(1,4),直接写出k的值和△PAB的面积;
(2)设直线PA、PB与x轴分别交于点M、N,求证:△PMN是等腰三角形;
(3)设点Q是反比例函数图象上位于P、B之间的动点(与点P、B不重合),连接AQ、BQ,比较∠PAQ与∠PBQ的大小,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
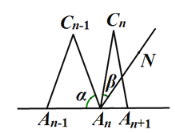
【题目】小知识:如图,我们称两臂长度相等(即![]() )的圆规为等臂圆规. 当等臂圆规的两脚摆放在一条直线上时,若张角
)的圆规为等臂圆规. 当等臂圆规的两脚摆放在一条直线上时,若张角![]() ,则底角
,则底角![]() .
.
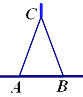
请运用上述知识解决问题:
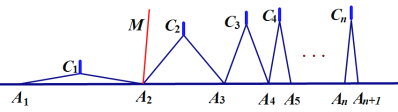
如图,![]() 个相同规格的等臂圆规的两脚依次摆放在同一条直线上,其张角度数变化如下:
个相同规格的等臂圆规的两脚依次摆放在同一条直线上,其张角度数变化如下:
![]() ,
,![]() ,
, ![]() ,
,![]() ,…
,…
(1)、①由题意可得![]() = ;
= ;
②若![]() 平分
平分![]() ,则
,则![]() = ;
= ;
(2)、![]() = (用含
= (用含![]() 的代数式表示);
的代数式表示);
(3)、当![]() 时,设
时,设![]() 的度数为
的度数为![]() ,
,![]() 的角平分线
的角平分线![]() 与
与![]() 构成的角的度数为
构成的角的度数为![]() ,那么
,那么![]() 与
与![]() 之间的等量关系是 ,请说明理由. (提示:可以借助下面的局部示意图)
之间的等量关系是 ,请说明理由. (提示:可以借助下面的局部示意图)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,给正五边形的顶点依次编号为1,2,3,4,5,若从某一个顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”,如:小明在编号为2的顶点上时,那么他应走2个边长,即从2→3→4为第一次“移位”,这时他到达编号为4的顶点,接下来他应走4个边长后从4→5→1→2→3为第二次“移位”若小明从编号为1的顶点开始,第2020次“移位”后,则他所处顶点的编号为
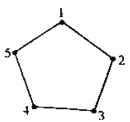
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】喜迎新年,某社区超市第一次用5000元购进甲、乙两种商品,其中甲商品件数是品的件数的2倍,甲、乙两种商品的进价和售价如下表:
甲 | 乙 | |
进价(元/件) | 15 | 20 |
售价(元/件) | 30 | 30 |
(1)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(2)能市第二次以第一次的进价又购进甲、乙两种商品,其中购进乙种商品的件数不变,购进甲种商品的件数是第一次购进甲种商品件数的2倍;乙商品按原价销售,甲商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多600元,求第二次甲种商品按原价打几折销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两车沿直路同向匀速行驶,甲、乙两车在行驶过程中离乙车出发地的路程![]() 与出发的时间
与出发的时间![]() 的函数关系加图1所示,两车之间的距离
的函数关系加图1所示,两车之间的距离![]() 与出发的时间
与出发的时间![]() 的函数关系如图2所示.
的函数关系如图2所示.
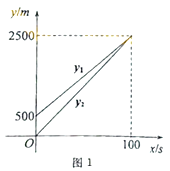
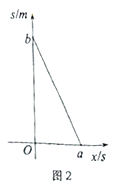
(1)图2中![]() __________,
__________,![]() __________;
__________;
(2)请用待定系数法求![]() 、
、![]() 关于
关于![]() 的函数解析式;(不用写自变量取值范围)
的函数解析式;(不用写自变量取值范围)
(3)出发多长时间,两车相距![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于任意四个有理数a,b,c,d,可以组成两个有理数对(a,b)与(c,d).我们规定:
(a,b)★(c,d)=bc-ad.
例如:(1,2)★(3,4)=2×3-1×4=2.
根据上述规定解决下列问题:
(1)有理数对(2,-3)★(3,-2)=_______;
(2)若有理数对(-3,2x-1)★(1,x+1)=7,则x=_______;
(3)当满足等式(-3,2x-1)★(k,x+k)=5+2k的x是整数时,求整数k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com