
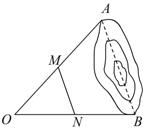
科目:初中数学 来源:不详 题型:解答题
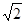 ,
,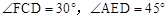 ,求DC的长.
,求DC的长.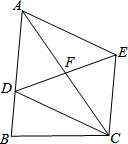
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
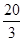 ,AE⊥BD,垂足是E.点F是点E关于AB的对称点,连接AF、BF.
,AE⊥BD,垂足是E.点F是点E关于AB的对称点,连接AF、BF.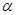 (0°<
(0°<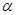 <180°),记旋转中的△ABF为△A′BF′,在旋转过程中,设A′F′所在的直线与直线AD交于点P.与直线BD交于点Q.是否存在这样的P、Q两点,使△DPQ为等腰三角形?若存在,求出此时DQ的长;若不存在,请说明理由.
<180°),记旋转中的△ABF为△A′BF′,在旋转过程中,设A′F′所在的直线与直线AD交于点P.与直线BD交于点Q.是否存在这样的P、Q两点,使△DPQ为等腰三角形?若存在,求出此时DQ的长;若不存在,请说明理由.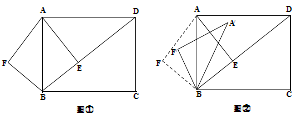
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
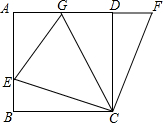
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
|
如图,矩形ABCD中,AB=5,AD=12,将矩形ABCD按如图所示的方式在直线 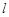 上进行两次旋转,则点B在两次旋转过程中经过的路径的长是( ) 上进行两次旋转,则点B在两次旋转过程中经过的路径的长是( )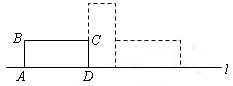
|
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.①③④ | B.①②④ | C.③④⑤ | D.②③⑤ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com