
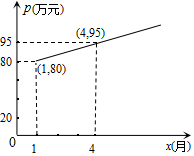
 在气候对人类生存压力日趋加大的今天,发展低碳经济,全面实现低碳生活成为人们的共识,某企业采用技术革新,节能减排,经分析前5个月二氧化碳排放量y(吨)与月份x(月)之间的函数关系是y=-2x+50.
在气候对人类生存压力日趋加大的今天,发展低碳经济,全面实现低碳生活成为人们的共识,某企业采用技术革新,节能减排,经分析前5个月二氧化碳排放量y(吨)与月份x(月)之间的函数关系是y=-2x+50.分析 (1)根据图象可以知道利润p(万元)与月份x是一次函数关系,并且随着月份的增加利润也增加,首先根据图象确定利润p与x的函数关系,然后利用函数的增减性即可确定今年哪月份,该企业获得的月利润最大?最大月利润是多少万元;
(2)由于该企业决定从今年6月份起,每月二氧化碳排放量在上一个月的基础上都下降a%,与此同时,每排放一吨二氧化碳,企业相应获得的利润在上一个月的基础上都增加50%.
解答 解:(1)根据图象知道当x=1,p=80,
当x=4,p=95,
设p=kx+b,
故$\left\{\begin{array}{l}{80=k+b}\\{95=4k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=5}\\{b=75}\end{array}\right.$,
则p=5x+75;根据k>0,p随x增大而增大,
∴当x=5时,p最大,p=5×5+75=100万元;
∴5月份的利润是:100万×40=4000万元;
(2)∵该企业决定从今年6月份起,每月二氧化碳排放量在上一个月的基础上都下降a%,
而当x=5时,y=40,
∴6月份的二氧化碳排放量为40(1-a%),
7月份的二氧化碳排放量为40(1-a%)2,
5月份的利润为4000万元,
∴6月份的利润为100(1+50%)×40(1-a%),
7月份的利润为100(1+50%)×(1+50%)×40(1-a%)2,
∴100(1+50%)×40(1-a%)+100(1+50%)×(1+50%)×40(1-a%)2=3×4000,
∴a=13.
点评 本题考查了二次函数的性质在实际生活中的应用. 这类题目我们首先要吃透题意,确定变量,建立函数模型,然后结合实际选择最优方案.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,∠ADE=∠ACB,且$\frac{AD}{AC}$=$\frac{2}{3}$,DE=10,则BC等于( )
如图,∠ADE=∠ACB,且$\frac{AD}{AC}$=$\frac{2}{3}$,DE=10,则BC等于( )| A. | 12 | B. | 15 | C. | 18 | D. | 20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
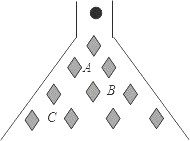 如图所示,当以实心小球从入口落下,它在依次碰到每层菱形挡块时,会等可能地向左或向右落下,求小球下落到第三层B位置的概率$\frac{3}{8}$.
如图所示,当以实心小球从入口落下,它在依次碰到每层菱形挡块时,会等可能地向左或向右落下,求小球下落到第三层B位置的概率$\frac{3}{8}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
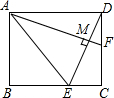 如图所示,在矩形ABCD中,F是DC上的一点,AE平分∠BAF交BC于点E,且DE⊥AF,垂足为点M,BE=3,AE=2$\sqrt{6}$,则MD的长是( )
如图所示,在矩形ABCD中,F是DC上的一点,AE平分∠BAF交BC于点E,且DE⊥AF,垂足为点M,BE=3,AE=2$\sqrt{6}$,则MD的长是( )| A. | $\sqrt{15}$ | B. | $\frac{{\sqrt{15}}}{15}$ | C. | 1 | D. | $\frac{{\sqrt{15}}}{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com