|
|
|
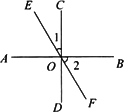
如图,直线AB、CD、EF相交于O点,且∠AOD=90°,∠1=40°,求∠2的度数.
|
|
|
答案:
解析:
|
解:因为∠AOD+∠AOC
=∠AOD+∠BOD
=180°,
所以∠AOD=∠AOC=∠BOD=90°,
又∠1+∠FOC=180°,
∠DOF+∠FOC=180°,
所以∠DOF=∠1=40°,
所以∠2=∠BOD-∠DOF=90°-40°=50°.
|
练习册系列答案
相关习题
科目:初中数学
来源:新人教版(2012) 七年级上
题型:
|
|
|
在∠AOB的内部任取一点C,作射线OC,则一定存在
|
| [ ] |
A. |
∠AOB>∠AOC
|
B. |
∠AOC>∠BOC
|
C. |
∠BOC>∠AOC
|
D. |
∠AOC=∠BOC
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 七年级上
题型:
|
|
|
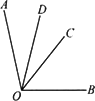
如图,OC是∠AOB的平分线,射线OD平分∠AOC,且∠AOB=98°,则∠COD为
|
| [ ] |
A. |
24°3
|
B. |
24°
|
C. |
29°
|
D. |
30°
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 七年级上
题型:
|
|
|
如图,已知∠BOC和∠AOB互补,又OD、OE分别是∠AOB和∠BOC的平分线,若∠AOB=55°,求∠DOE的度数,∠AOB(小于平角)的大小对∠DOE的大小有影响吗?
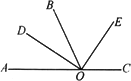
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 七年级上
题型:
|
|
|
(探究题)(1)如图,如果∠AOC=∠BOD=78°,∠DOC=29°,求∠AOD和∠BOC的度数;
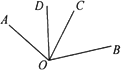
(2)在(1)中,只要知道∠AOC=∠BOD,就可以得出∠AOD和∠BOC一定相等,这是为什么?
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 七年级上
题型:
|
|
|
已知∠A=37°,则∠A的余角等于
|
| [ ] |
A. |
37°
|
B. |
53°
|
C. |
63°
|
D. |
143°
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 七年级上
题型:
|
|
|
有五个点,每三个点都不在一条直线上,过其中每两个点画直线,可以画________条直线.
|
|
|
查看答案和解析>>
