

分析 根据旋转的性质求解.
旋转的性质是旋转不改变图形的大小和形状.
解答 解:∵BC=3,
∴图1中点C的坐标为(4,3),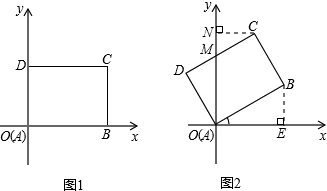
在图2中,设CD与y轴交于点M,作CN⊥y轴于点N,那么∠DOM=30°,OD=3,
∴DM=3•tan30°=$\sqrt{3}$,OM=3÷cos30°=2$\sqrt{3}$,
那么CM=4-$\sqrt{3}$,易知∠NCM=30°,
∴MN=CM•sin30°=$\frac{4-\sqrt{3}}{2}$,CN=CM•cos30°=$\frac{4\sqrt{3}-3}{2}$,
则ON=OM+MN=$\frac{3\sqrt{3}+4}{2}$,
∴图2中C点的坐标为($\frac{4\sqrt{3}-3}{2}$,$\frac{3\sqrt{3}+4}{2}$).
故答案为:($\frac{4\sqrt{3}-3}{2}$,$\frac{3\sqrt{3}+4}{2}$).
点评 此题考查旋转问题,关键是根据旋转前后对应角的度数不变,对应线段的长度不变,注意构造直角三角形求解.


科目:初中数学 来源: 题型:选择题
| A. | a<-$\frac{9}{4}$ | B. | a≥-$\frac{9}{4}$且a≠0 | C. | a>-$\frac{9}{4}$且a≠0 | D. | a>-$\frac{9}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,AB是⊙O的弦,AB=7$\sqrt{2}$,点C是⊙O上的一动点,且∠ACB=45°.若点M,N分别是AB,BC的中点,则MN长的最大值是7.
如图,AB是⊙O的弦,AB=7$\sqrt{2}$,点C是⊙O上的一动点,且∠ACB=45°.若点M,N分别是AB,BC的中点,则MN长的最大值是7.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图CA=CD,CB=CE,欲证△ABC≌△DEC,可补充条件( )
如图CA=CD,CB=CE,欲证△ABC≌△DEC,可补充条件( )| A. | ∠BCE=∠ACD | B. | ∠B=∠E | C. | ∠A=∠D | D. | ∠BCA=∠ACD |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=7,b=24,c=25 | B. | a=1.5,b=2,c=2.5 | C. | a=$\frac{1}{3}$,b=$\frac{1}{4}$,c=$\frac{1}{5}$ | D. | a=15,b=8,c=17 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com