
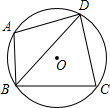
 如图,⊙O过四边形ABCD的四个顶点,已知∠ABC=90°,BD平分∠ABC,AB=1,BC=2,则AD=
如图,⊙O过四边形ABCD的四个顶点,已知∠ABC=90°,BD平分∠ABC,AB=1,BC=2,则AD=
| ||
| 2 |
| ||
| 2 |
| 5 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
3
| ||
| 2 |
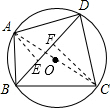 解:如图,连结AC.
解:如图,连结AC. |
| AD |
 |
| CD |
| ||
| 2 |
| ||
| 2 |
| 5 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
3
| ||
| 2 |
| ||
| 2 |
3
| ||
| 2 |


科目:初中数学 来源: 题型:
| A、460 | B、455 |
| C、450 | D、0 |
查看答案和解析>>
科目:初中数学 来源: 题型:
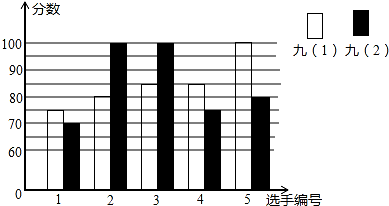
| 班级 | 平均数(分) | 中位数(分) | 众数(分) |
| 九(1) | 85 | ||
| 九(2) | 85 | 100 |
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图是一个经过改造的台球桌面的示意图,图中四个角上的黑色部分分别表示四个人球孔.如果一个球按图中所示的方向被击出(球可以经过多次反弹),那么该球最后将落入的球袋是
如图是一个经过改造的台球桌面的示意图,图中四个角上的黑色部分分别表示四个人球孔.如果一个球按图中所示的方向被击出(球可以经过多次反弹),那么该球最后将落入的球袋是查看答案和解析>>
科目:初中数学 来源: 题型:
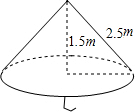 一把大遮阳伞,伞面撑开时可近似地看成是圆锥形,如图,它的母线长是2.5m,高为1.5m,则做这把遮阳伞需用布料的面积(不计接缝)是( )
一把大遮阳伞,伞面撑开时可近似地看成是圆锥形,如图,它的母线长是2.5m,高为1.5m,则做这把遮阳伞需用布料的面积(不计接缝)是( )| A、3πm2 | ||
| B、4πm2 | ||
| C、5πm2 | ||
D、
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com