
 �������״����ܡ�֮�����˱���������û�����٣��ܽᷴ˼���ڹ�Լ������һ����ͼ�еĺ���ͼ��̻����ڹ����е�·��y1��������е�ʱ��x�Ĺ�ϵ��
�������״����ܡ�֮�����˱���������û�����٣��ܽᷴ˼���ڹ�Լ������һ����ͼ�еĺ���ͼ��̻����ڹ����е�·��y1��������е�ʱ��x�Ĺ�ϵ������ ��1�����ݺ���ͼ����Խ���⣻
��2������������Ի���y2��x�ĺ���ͼ��
��3������������Էֱ����y2��y2��Ӧ�ĺ�������ʽ��Ȼ����������ȼ��ɽ���⣮
��� 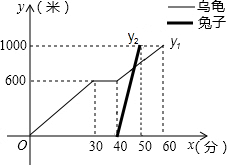 �⣺��1����ͼ��ɵã�
�⣺��1����ͼ��ɵã�
�������ٴ����ܡ���·��Ϊ1000�ף��ڹ���;����Ϣ��40-30=10���ӣ��ڹ�����ȫ������60���ӣ�
�ʴ�Ϊ��1000��10��60��
��2������ͼ��ʾ��
��3�������ӵ�·��y2��ʱ��x�Ĺ�ϵʽΪy2=kx+b��40��x��50��
$\left\{\begin{array}{l}{40k+b=0}\\{50k+b=1000}\end{array}\right.$����$\left\{\begin{array}{l}{k=100}\\{b=-4000}\end{array}\right.$��
����y2=100x-4000��
���ڹ���40-60���ӵ�·��y1��ʱ��x�Ĺ�ϵʽΪy1=mx+n��40��x��60��
$\left\{\begin{array}{l}{40m+n=600}\\{60m+n=1000}\end{array}\right.$����$\left\{\begin{array}{l}{m=20}\\{n=-200}\end{array}\right.$��
����y1=20x-200��
��y1=y2ʱ���������ڹ꣬
��ʱ20x-200=100x-4000��
��ã�x=47.5��
��y1=y2=20��47.5-200=750�ף�
����������750�����ڹ꣮
���� ���⿼��һ�κ�����Ӧ�ã������Ĺؼ�����ȷ���⣬�����Ӧ�ĺ�������ʽ������һ�κ��������ʺ����ν�ϵ�˼����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
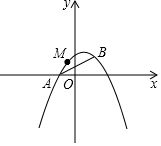 ��ͼ����֪������y=ax2+bx+1����A��-1��0����B��1��1�����㣮
��ͼ����֪������y=ax2+bx+1����A��-1��0����B��1��1�����㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| ��Ա1 | ��Ա2 | ��Ա3 | ��Ա4 | |
| ���� | 176 | 177 | 175 | 176 |
| ���� | 178 | 175 | 177 | 174 |
| A�� | $\overline{x_��}��\overline{x_��}��S_��^2��S_��^2$ | B�� | $\overline{x_��}=\overline{x_��}��S_��^2��S_��^2$ | ||
| C�� | $\overline{x_��}��\overline{x_��}��S_��^2��S_��^2$ | D�� | $\overline{x_��}=\overline{x_��}��S_��^2��S_��^2$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
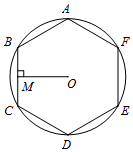 ��ͼ����������ABCDEF�ڽ���ԲO���뾶Ϊ4��������������εı��ľ�OM�ͻ�BC�ij��ֱ�Ϊ��������
��ͼ����������ABCDEF�ڽ���ԲO���뾶Ϊ4��������������εı��ľ�OM�ͻ�BC�ij��ֱ�Ϊ��������| A�� | 2$\sqrt{3}$��$\frac{4��}{3}$ | B�� | 2$\sqrt{3}$���� | C�� | $\sqrt{3}$��$\frac{2��}{3}$ | D�� | 2��$\frac{��}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ������˾Ϊ���������Լ�õ磬��ȡ�����õ����ֶ��շѵİ취����֪ij������ÿ��Ӧ�ɵ��y��Ԫ�����õ���x���ȣ��ĺ���ͼ����һ�����ߣ���ͼ��������ͼ�����������⣮
������˾Ϊ���������Լ�õ磬��ȡ�����õ����ֶ��շѵİ취����֪ij������ÿ��Ӧ�ɵ��y��Ԫ�����õ���x���ȣ��ĺ���ͼ����һ�����ߣ���ͼ��������ͼ�����������⣮�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com