
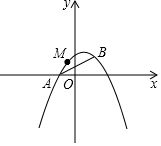
 如图,已知抛物线y=ax2+bx+1经过A(-1,0),B(1,1)两点.
如图,已知抛物线y=ax2+bx+1经过A(-1,0),B(1,1)两点.分析 (1)根据待定系数法,可得函数解析式;
(2)根据垂线间的关系,可得PA,PB的解析式,根据解方程组,可得P点坐标;
(3)根据垂直于x的直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得MQ,根据三角形的面积,可得二次函数,根据二次函数的性质,可得面积的最大值,根据三角形的底一定时面积与高成正比,可得三角形高的最大值.
解答 解:(1)将A,B点坐标代入,得
$\left\{\begin{array}{l}{a-b+1=0①}\\{a+b+1=1②}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=\frac{1}{2}}\end{array}\right.$,
抛物线的解析式为y=-$\frac{1}{2}$x2+$\frac{1}{2}$x+1;
(2)①由直线y=3x-1与直线y=mx+2互相垂直,得
3m=-1,
即m=-$\frac{1}{3}$;
②AB的解析式为y=$\frac{1}{2}$x+$\frac{1}{2}$,
当PA⊥AB时,PA的解析式为y=-2x-2,
联立PA与抛物线,得
$\left\{\begin{array}{l}{y=-\frac{1}{2}{x}^{2}+\frac{1}{2}x+1}\\{y=-2x-2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=-1}\\{y=0}\end{array}\right.$(舍),$\left\{\begin{array}{l}{x=6}\\{y=-14}\end{array}\right.$,即P(6,-14);
当PB⊥AB时,PB的解析式为y=-2x+3,
联立PB与抛物线,得$\left\{\begin{array}{l}{y=-\frac{1}{2}{x}^{2}+\frac{1}{2}x+1}\\{y=-2x+3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$(舍)$\left\{\begin{array}{l}{x=4}\\{y=-5}\end{array}\right.$即P(4,-5),
综上所述:△PAB是以AB为直角边的直角三角形,点P的坐标(6,-14)(4,-5);
(3)如图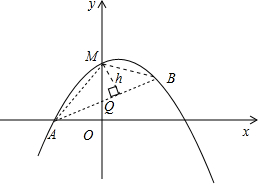 ,
,
∵M(t,-$\frac{1}{2}$t2+$\frac{1}{2}$t+1),Q(t,$\frac{1}{2}$t+$\frac{1}{2}$),
∴MQ=-$\frac{1}{2}$t2+$\frac{1}{2}$
S△MAB=$\frac{1}{2}$MQ|xB-xA
=$\frac{1}{2}$(-$\frac{1}{2}$t2+$\frac{1}{2}$)×2
=-$\frac{1}{2}$t2+$\frac{1}{2}$,
当t=0时,S取最大值$\frac{1}{2}$,即M(0,1).
由勾股定理,得
AB=$\sqrt{(1+1)^{2}+{1}^{2}}$=$\sqrt{5}$,
设M到AB的距离为h,由三角形的面积,得
h=$\frac{1}{\sqrt{5}}$=$\frac{\sqrt{5}}{5}$.
点M到直线AB的距离的最大值是$\frac{\sqrt{5}}{5}$.
点评 本题考查了二次函数综合题,解(1)的关键是待定系数法,解(2)的关键是利用垂线间的关系得出直线PA,或PB的解析式,又利用解方程组;解(3)的关键是利用三角形的底一定时面积与高成正比得出最大面积时高最大.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:解答题
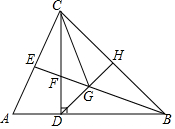 如图,在△ABC中,AB=BC,BE平分∠ABC,CD⊥AB于点D,CD=BD,点H是BC边的中点,连接DH,交BE于点G,连接CG.
如图,在△ABC中,AB=BC,BE平分∠ABC,CD⊥AB于点D,CD=BD,点H是BC边的中点,连接DH,交BE于点G,连接CG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
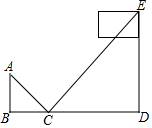 处看到旗杆顶部E,此时小军的站立点B与点C的水平距离为2m,旗杆底部D与点C的水平距离为12m.若小军的眼睛距离地面的高度为1.5m(即AB=1.5m),则旗杆的高度为9m.
处看到旗杆顶部E,此时小军的站立点B与点C的水平距离为2m,旗杆底部D与点C的水平距离为12m.若小军的眼睛距离地面的高度为1.5m(即AB=1.5m),则旗杆的高度为9m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
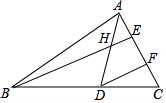 如图,在△ABC中,∠ABC=36°,∠C=64°,AD平分∠BAC,交BC于D,BE⊥AC,交AD、AC于H、E,且DF∥BE.
如图,在△ABC中,∠ABC=36°,∠C=64°,AD平分∠BAC,交BC于D,BE⊥AC,交AD、AC于H、E,且DF∥BE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 “龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场,图中的函数图象刻画了乌龟所行的路程y1与出发所行的时间x的关系.
“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场,图中的函数图象刻画了乌龟所行的路程y1与出发所行的时间x的关系.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3×108 | B. | 0.3×108 | C. | 3×109 | D. | 0.3×109 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com