
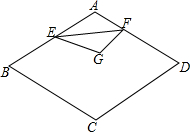
 如图,已知菱形ABCD中,∠BAD=120°,AB=2,E、F分别是线段AB、AD上的动点,若以EF为折线翻折,点A落在菱形ABCD所在平面的G点位置,则点G所有可能出现的区域的面积是$\frac{4}{3}$π-2$\sqrt{3}$.
如图,已知菱形ABCD中,∠BAD=120°,AB=2,E、F分别是线段AB、AD上的动点,若以EF为折线翻折,点A落在菱形ABCD所在平面的G点位置,则点G所有可能出现的区域的面积是$\frac{4}{3}$π-2$\sqrt{3}$. 分析 以EF为折线翻折,A点落在菱形ABCD所在的G点的位置,那么G所有可能位置形成的图形是图中阴影部分.根据S阴=2•S扇形BAC-S菱形ABCD计算即可.
解答 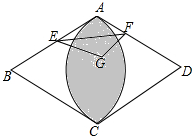 解:如图,以EF为折线翻折,点A落在菱形ABCD所在平面的G点位置,
解:如图,以EF为折线翻折,点A落在菱形ABCD所在平面的G点位置,
则点G所有可能出现的区域是图中阴影.
∵四边形ABCD是菱形,∠BAD=120°,
∴∠B=60°,
∴S阴=2•S扇形BAC-S菱形ABCD=2×$\frac{60π×{2}^{2}}{360}$-2×$\sqrt{3}$=$\frac{4}{3}$π-2$\sqrt{3}$,
故答案为:$\frac{4}{3}$π-2$\sqrt{3}$.
点评 本题考查翻折变换、扇形的面积公式、菱形的性质等知识,解题的关键是正确判断G所有可能位置形成的图形,属于中考填空题中的压轴题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
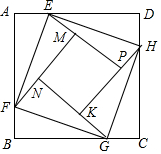 如图正方形ABCD的边长为2,点E,F,G,H分别在AD,AB,BC,CD上,且EA=FB=GC=HD,分别将△AEF,△BFG,△CGH,△DHE沿EF,FG,GH,HE翻折,得四边形MNKP,设AE=x(0<x<1),S四边形MNKP=y,则y关于x的函数图象大致为( )
如图正方形ABCD的边长为2,点E,F,G,H分别在AD,AB,BC,CD上,且EA=FB=GC=HD,分别将△AEF,△BFG,△CGH,△DHE沿EF,FG,GH,HE翻折,得四边形MNKP,设AE=x(0<x<1),S四边形MNKP=y,则y关于x的函数图象大致为( )| A. | 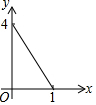 | B. | 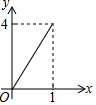 | C. | 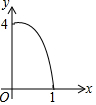 | D. | 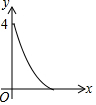 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 49(1+x)2=36 | B. | 36(1-x)2=49 | C. | 36(1+x)2=49 | D. | 49(1-x)2=36 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.608×106 | B. | 6.08×105 | C. | 6.08×106 | D. | 60.8×104 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平均数 | B. | 中位数 | C. | 方差 | D. | 众数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com