
 如图所示,△ABC中,E、F、D分别是边AB、AC、BC上的点,且满足
如图所示,△ABC中,E、F、D分别是边AB、AC、BC上的点,且满足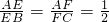 ,则△EFD与△ABC的面积比为
,则△EFD与△ABC的面积比为



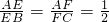 ,根据比例性质易得
,根据比例性质易得 =
= =
= ,而∠A=∠A,易证△AEF∽△ABC,从而易得h′=3h,那么△DEF的高就是2h,再设△AEF的面积是s,EF=a,由于相似三角形的面积比等于相似比的平方,那么S△AEF:S△ABC=1:9,于是S△ABC=9s,根据三角形面积公式易求S△DEF=2s,从而易求S△DEF:S△ABC的值.
,而∠A=∠A,易证△AEF∽△ABC,从而易得h′=3h,那么△DEF的高就是2h,再设△AEF的面积是s,EF=a,由于相似三角形的面积比等于相似比的平方,那么S△AEF:S△ABC=1:9,于是S△ABC=9s,根据三角形面积公式易求S△DEF=2s,从而易求S△DEF:S△ABC的值. ∵
∵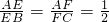 ,
, =
= =
= ,
,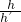 =
= ,S△AEF:S△ABC=1:9,
,S△AEF:S△ABC=1:9, •EF•2h=ah=2s,
•EF•2h=ah=2s,

 名校课堂系列答案
名校课堂系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com