Question

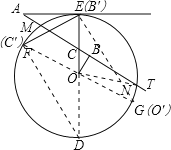
【题目】如图，AE切⊙O于点E，AT交⊙O于点M，N，线段OE交AT于点C，OB⊥AT于点B，已知∠EAT=30°，AE=，MN=．

（1）求∠COB的度数；

（2）求⊙O的半径R；

（3）点F在⊙O上（是劣弧），且EF=5，把△OBC经过平移、旋转和相似变换后，使它的两个顶点分别与点E，F重合．在EF的同一侧，这样的三角形共有多少个？你能在其中找出另一个顶点在⊙O上的三角形吗？请在图中画出这个三角形，并求出这个三角形与△OBC的周长之比．

Answer 1

【答案】（1）30°；（2）5；（3）6个，5：1．

【解析】

试题分析：（1）由AE与圆O相切，根据切线的性质得到AE与CE垂直，又OB与AT垂直，可得出两直角相等，再由一对对顶角相等，利用两对对应角相等的两三角形相似可得出三角形AEC与三角形OBC相似，根据相似三角形的对应角相等可得出所求的角与∠A相等，由∠A的度数即可求出所求角的度数；

（2）在直角三角形AEC中，由AE及tanA的值，利用锐角三角函数定义求出CE的长，再由OB垂直于MN，由垂径定理得到B为MN的中点，根据MN的长求出MB的长，在直角三角形OBM中，由半径OM=R，及MB的长，利用勾股定理表示出OB的长，在直角三角形OBC中，由表示出OB及cos30°的值，利用锐角三角函数定义表示出OC，用OE﹣OC=EC列出关于R的方程，求出方程的解得到半径R的值；

（3）把△OBC经过平移、旋转和相似变换后，使它的两个顶点分别与点E，F重合，在EF的同一侧，这样的三角形共有3个．延长EO与圆交于点D，连接DF，如图所示，由第二问求出半径，的长直径ED的长，根据ED为直径，利用直径所对的圆周角为直角，得到三角形EFD为直角三角形，由∠FDE为30°，利用锐角三角函数定义求出DF的长，表示出三角形EFD的周长，再由第二问求出的三角形OBC的三边表示出三角形BOC的周长，即可求出两三角形的周长之比．

试题解析：（1）∵AE切⊙O于点E，∴AE⊥CE，又OB⊥AT，∴∠AEC=∠CBO=90°，又∠BCO=∠ACE，∴△AEC∽△OBC，又∠A=30°，∴∠COB=∠A=30°；

（2）∵AE=，∠A=30°，∴在Rt△AEC中，tanA=tan30°=，即EC=AEtan30°=3，∵OB⊥MN，∴B为MN的中点，又MN=，∴MB=MN=，连接OM，在△MOB中，OM=R，MB=，∴OB==，在△COB中，∠BOC=30°，∵cos∠BOC=cos30°==，∴BO=OC，∴OC=OB=，又OC+EC=OM=R，∴R=+3，整理得：，即（R+23）（R﹣5）=0，解得：R=﹣23（舍去）或R=5，则R=5；

（3）以EF为斜边，有两种情况，以EF为直角边，有四种情况，所以六种，画直径FG，连接EG，延长EO与圆交于点D，连接DF，如图所示：

∵EF=5，直径ED=10，可得出∠FDE=30°，∴FD=，则C△EFD=5+10+=15+，由（2）可得C△COB=，∴C△EFD：C△COB=（）：（）=5：1．

∵EF=5，直径FG=10，可得出∠FGE=30°，∴EG=，则C△EFG=5+10+=15+，∴C△EFG：C△COB=（）：（）=5：1．