
分析 (1)利用△≥0可得结论;
(2)先判断x1、x2为方程x2-3(m-1)x+3m-4=0的两根,根据根与系数的关系得x1+x2=3(m-1),x1•x2=3m-4,再由$\frac{1}{OA}$+$\frac{1}{OB}$=$\frac{2}{OA}$•$\frac{1}{OB}$,得到|x1|+|x2|=2,接着分类讨论x1和x2的符号去绝对值得到m的方程,然后解方程求出满足条件的m的值.
解答 (1)证明:△=[-3(m-1)]2-4×1×(3m-4)
=9m2-30m+25
=(3m-5)2
∵(3m-5)2≥0,
∴不论m为何实数,方程总有两个实数根;
(2)(2)根据题意,x1、x2为方程x2-3(m-1)x+3m-4=0的两根,
∴x1+x2=3(m-1),x1•x2=3m-4,
∵$\frac{1}{OA}$+$\frac{1}{OB}$=$\frac{2}{OA}$•$\frac{1}{OB}$,
∴OA+OB=2,
而OA=|x1|,OB=|x2|,
∴|x1|+|x2|=2,
当x1+x2=3(m-1)>0,x1•x2=3m-4>0,即m>$\frac{4}{3}$且m≠$\frac{5}{3}$,则3(m-1)=2,解得m=$\frac{5}{3}$(舍去);
当x1+x2=3(m-1)<0,x1•x2=3m-4>0,m的值不存在;
当x1•x2=3m-4<0,即m<$\frac{4}{3}$,则x1与x2异号,x12+x22-2x1x2=4,
∴(x1+x2)2-4x1x2=4,
∴9(m-1)2-4(3m-4)=4,
整理得3m2-10m+7=0,解得m1=$\frac{7}{3}$(舍去),m2=1,
∴m的值为1.
点评 本题考查了抛物线与x轴的交点,也考查了根的判别式和根与系数的关系:关键是把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标转化为解关于x的一元二次方程.对于二次函数y=ax2+bx+c(a,b,c是常数,a≠0),△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:选择题
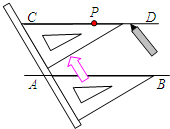 如图,给出了过直线AB外一点P,作已知直线AB的平行线的方法,其依据是( )
如图,给出了过直线AB外一点P,作已知直线AB的平行线的方法,其依据是( )| A. | 同位角相等,两直线平行 | |
| B. | 内错角相等,两直线平行 | |
| C. | 同旁内角互补,两直线品行 | |
| D. | 过直线外一点有且只有一条直线与这条直线平行 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
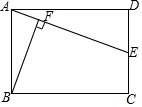 如图,在矩形ABCD中,AB=2,BC=3.若点E是边CD的中点,连接AE,过点B作BF⊥AE交AE于点F,则BF的长为( )
如图,在矩形ABCD中,AB=2,BC=3.若点E是边CD的中点,连接AE,过点B作BF⊥AE交AE于点F,则BF的长为( )| A. | $\frac{3\sqrt{10}}{2}$ | B. | $\frac{3\sqrt{10}}{5}$ | C. | $\frac{\sqrt{10}}{5}$ | D. | $\frac{3\sqrt{5}}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE=5$\sqrt{5}$cm,且tan∠EFC=0.75,则矩形ABCD的周长为36cm.
如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE=5$\sqrt{5}$cm,且tan∠EFC=0.75,则矩形ABCD的周长为36cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
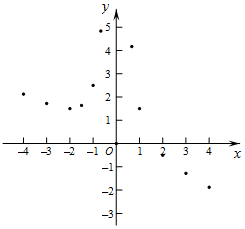 有这样一个问题:探究函数y=$\frac{2}{{x}^{2}}$-$\frac{1}{2}$x的图象与性质.
有这样一个问题:探究函数y=$\frac{2}{{x}^{2}}$-$\frac{1}{2}$x的图象与性质.| x | … | -4 | -3 | -2 | -$\frac{3}{2}$ | -1 | -$\frac{2}{3}$ | $\frac{2}{3}$ | 1 | 2 | 3 | 4 | … |
| y | … | $\frac{17}{8}$ | $\frac{31}{18}$ | $\frac{3}{2}$ | $\frac{59}{36}$ | $\frac{5}{2}$ | $\frac{29}{6}$ | $\frac{25}{6}$ | $\frac{3}{2}$ | -$\frac{1}{2}$ | -$\frac{23}{18}$ | m | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com