【题目】如图，已知四边形ABCD中，∠D＝∠B＝90°，AE平分∠DAB，CF平分∠DCB
（1）若∠DAB＝72°，∠2＝ °，∠3＝ °；
（2）求证：AE∥CF．
【答案】（1）54，36；（2）证明见解析.
【解析】
（1）求出∠DAB+∠DCB=180°，求出∠2+∠1=90°，然后即可求出∠2和∠3的度数；
（2）推出∠1=∠3，根据平行线的判定得出即可.
（1）解：∵∠DAB+∠DCB+∠D+∠B＝360°，∠D＝∠B＝90°，
∴∠DAB+∠DCB＝360°﹣（∠D+∠B）＝180°，
∵AE平分∠DAB，CF平分∠DCB，∠DAB＝72°，
∴∠1＝
∠DAB＝36°，∠2＝∠DCB，
∴∠1+∠2＝（∠DAB+∠DCB）＝90°，
∴∠2＝54°，
∵∠3+∠2+∠B＝180°，
∴∠3＝180°﹣∠B﹣∠2＝180°﹣90°﹣54°＝36°，
故答案为：54，36；
（2）证明：由（1）得∴∠1＝36°，∠3＝36°，
∴∠1＝∠3，
∴AE∥CF．
阅读快车系列答案科目：初中数学 来源： 题型：
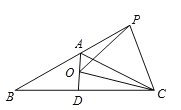
【题目】如图，已知等腰△ABC中，AB=AC，∠BAC=120°，AD⊥BC于点D，点P是BA延长线上一点，点O是线段AD上一点，OP=OC，下面的结论：
①∠APO+∠DCO=30°；②△OPC是等边三角形：③AC=DO+AP；④S△ABC=S四形形AOCP．
其中正确的是_______．（填序号）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知△ABC中，AB=AC，把△ABC绕A点沿顺时针方向旋转得到△ADE，连接BD，CE交于点F． 
（1）求证：△AEC≌△ADB；
（2）若AB=2，∠BAC=45°，当四边形ADFC是菱形时，求BF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在矩形
中，
是
的中点，将
沿
折叠后得到
，点
在矩形内部，延长
交
于点G．
（1）猜想线段
与
有何数量关系？并证明你的结论；
（2）若
，
，求线段的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）如图1所示，△ABC中，∠ACB的角平分线CF与∠EAC的角平分线AD的反向延长线交于点F；
①若∠B＝90°则∠F＝ ；
②若∠B＝a，求∠F的度数（用a表示）；
（2）如图2所示，若点G是CB延长线上任意一动点，连接AG，∠AGB与∠GAB的角平分线交于点H，随着点G的运动，∠F+∠H的值是否变化？若变化，请说明理由；若不变，请求出其值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=AC=24厘米，BC=16厘米，点D为AB的中点，点P在线段BC上以4厘米/秒的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．当点Q的运动速度为_______厘米/秒时，能够在某一时刻使△BPD与△CQP全等．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，AC∥DF，直线AF分别与直线BD、CE相交于点G，H，∠1＝∠2，求证：∠C＝∠D．
解：∵∠1＝∠2（已知）
∠1＝∠DGH（ ），
∴∠2＝ （ 等量代换 ）
∴ ∥ （同位角相等，两直线平行）
∴∠C＝ （两直线平行，同位角相等）
又∵AC∥DF（ ）
∴∠D＝∠ABG （ ）
∴∠C＝∠D （ ）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
