【题目】已知：如图，AC∥DF，直线AF分别与直线BD、CE相交于点G，H，∠1＝∠2，求证：∠C＝∠D．
解：∵∠1＝∠2（已知）
∠1＝∠DGH（ ），
∴∠2＝ （ 等量代换 ）
∴ ∥ （同位角相等，两直线平行）
∴∠C＝ （两直线平行，同位角相等）
又∵AC∥DF（ ）
∴∠D＝∠ABG （ ）
∴∠C＝∠D （ ）
津桥教育计算小状元系列答案科目：初中数学 来源： 题型：
【题目】如图，已知四边形ABCD中，∠D＝∠B＝90°，AE平分∠DAB，CF平分∠DCB
（1）若∠DAB＝72°，∠2＝ °，∠3＝ °；
（2）求证：AE∥CF．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E,∠ADC=70°.
(1)求∠EDC的度数;
(2)若∠ABC=n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示);若不改变,请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD内接于⊙O，AB是⊙O的直径，点P在CA的延长线上，∠CAD=45°．
（Ⅰ）若AB=4，求 
的长；
（Ⅱ）若 
= 
，AD=AP，求证：PD是⊙O的切线．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD的对角线AC、BD相交于点O，△ABO≌△ADO，下列结论：①AC⊥BD；②CB=CD；③△ABC≌△ADC；④DA=DC．其中所有正确结论的个数有（ ）
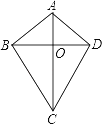
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AN是⊙M的直径，NB∥x轴，AB交⊙M于点C． 
（1）若点A（0，6），N（0，2），∠ABN=30°，求点B的坐标；
（2）若D为线段NB的中点，求证：直线CD是⊙M的切线．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们定义：
（概念理解）
在一个三角形中，如果一个角的度数是另一个角度数的 4 倍，那么这样的三角形我们称之为“完美三角形”．如：三个内角分别为 130°，40°，10°的三角形是“完美三角形”.
（简单应用）
如图 1，∠MON=72°，在射线OM上找一点A，过点A作AB⊥OM 交ON于点B，以A为端点作射线AD，交线段OB 于点C（点 C不与 O，B重合）
（1）∠ABO＝ ，△AOB__________（填“是”或“不是”）“完美三角形”；
（2）若∠ACB＝90°，求证：△AOC是“完美三角形”．
（应用拓展）
如图 2，点D在△ABC 的边AB上，连接DC，作∠ADC的平分线交AC于点E，在DC上取点F，使
，
．若△BCD是“完美三角形”， 求∠B的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】矩形ABCD中，对角线AC和BD相交于O，∠AOB＝60度，AC＝10，（1）求矩形较短边的长．
（2）矩形较长边的长
（3）矩形的面积
如果把本题改为：矩形ABCD中，对角线AC和BD相交于O，∠AOB＝60度，AB＝4，你能求出这个矩形的面积吗？试写出解答过程．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，四边形ABCD的四个顶点的坐标分别是A（1，3）、B（2，2）、C（2，1），D（3，3）．
（1）以原点O为位似中心，相似比为2，将图形放大，画出符合要求的位似四边形；
（2）在（1）的前提下，写出点A的对应点坐标A′，并说明点A与点A′坐标的关系．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
