
【题目】如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E,∠ADC=70°.
(1)求∠EDC的度数;
(2)若∠ABC=n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示);若不改变,请说明理由.

【答案】(1)35°.;(2)![]() n°+35°.(3)215°-
n°+35°.(3)215°-![]() n°.
n°.
【解析】试题分析:(1)、根据角平分线直接得出答案;(2)、过点E作EF∥AB,然后根据平行线的性质和角平分线的性质求出角度;(3)、首先根据题意画出图形,然后过点E作EF∥AB,按照第二小题同样的方法进行计算角度.
试题解析:(1)、∵DE平分∠ADC,∠ADC=70°,
∴∠EDC=![]() ∠ADC=
∠ADC=![]() ×70°=35°;
×70°=35°;
(2)、过点E作EF∥AB,

∵AB∥CD,
∴AB∥CD∥EF,
∴∠ABE=∠BEF,∠CDE=∠DEF,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=70°,
∴∠ABE=![]() ∠ABC=
∠ABC=![]() n°,∠CDE=
n°,∠CDE=![]() ∠ADC=35°,
∠ADC=35°,
∴∠BED=∠BEF+∠DEF=![]() n°+35°;
n°+35°;
(3)、过点E作EF∥AB
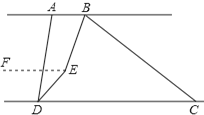
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=70°
∴∠ABE=![]() ∠ABC=
∠ABC=![]() n°,∠CDE=
n°,∠CDE=![]() ∠ADC=35°
∠ADC=35°
∵AB∥CD,
∴AB∥CD∥EF,
∴∠BEF=180°-∠ABE=180°-![]() n°,∠CDE=∠DEF=35°,
n°,∠CDE=∠DEF=35°,
∴∠BED=∠BEF+∠DEF=180°-![]() n°+35°=215°-
n°+35°=215°-![]() n°.
n°.


科目:初中数学 来源: 题型:
【题目】如图,在折纸活动中,小明制作了一张⊿ABC纸片,点D、E分别是边AB、AC上,将⊿ABC沿着DE折叠压平,A与A’重合,若∠A=75°,则∠1+∠2=( )
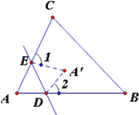
A. 150° B. 210° C. 105° D. 75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1, ![]() 的角平分线BD、CE相交于点P.
的角平分线BD、CE相交于点P.
(1)如果![]() ,求∠BPC的度数;
,求∠BPC的度数;
(2)如图2,作![]() 外角
外角![]() 的角平分线交于点Q,试探索
的角平分线交于点Q,试探索![]() 、
、![]() 之间的数量关系。
之间的数量关系。
(3)如图3,延长线段BP、QC交于点E,△BQE中,存在一个内角等于另一个内角的2倍,求![]() 的度数
的度数

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是9×7的正方形点阵,其水平方向和竖起直方向的两格点间的长度都为1个单位,以这些点为顶点的三角形称为格点三角形.请通过画图分析、探究回答下列问题:

(1)请在图中画出以AB为边且面积为2的一个网格三角形;
(2)任取该网格中能与A、B构成三角形的一点M,求以A、B、M为顶点的三角形的面积为2的概率;
(3)任取该网格中能与A、B构成三角形的一点M,求以A、B、M为顶点的三角形为直角三角形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.
(1)若∠A=60°,∠ABD=24°,求∠ACF的度数;
(2)若EF=4,BF:FD=5:3,S△BCF=10,求点D到AB的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,AB=6cm,AD=24cm,BC与CD的长度之和为34cm,其中C是直线l上的一个动点,请你探究当C离点B有多远时,△ACD是以DC为斜边的直角三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在13×13的网格图中,已知△ABC和点M(1,2).
(1)以点M为位似中心,画出△ABC的位似图形△A′B′C′,其中△A′B′C′与△ABC的位似比为2;
(2)写出△A′B′C′的各顶点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
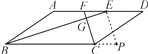
【题目】如图,在ABCD中,∠ABC、∠BCD的平分线BE、CF分别与AD相交于点E、F,BE与CF相交于点G.
(1)求证:BE⊥CF;
(2)若AB=3,BC=5,CF=2,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=a°.则下列结论: ①∠BOE=![]() (180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论__________(填编号).
(180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论__________(填编号).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com