
【题目】如图,在折纸活动中,小明制作了一张⊿ABC纸片,点D、E分别是边AB、AC上,将⊿ABC沿着DE折叠压平,A与A’重合,若∠A=75°,则∠1+∠2=( )
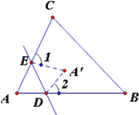
A. 150° B. 210° C. 105° D. 75°
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
【题目】在宿州十一中校园文化艺术节中,九年级十班有1名男生和2名女生获得美术奖,另有2名男生和2名女生获得音乐奖.
(1)从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会,求刚好是男生的概率;
(2)分别从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会,用列表或树状图求刚好是一男生一女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将下列方格纸中的△ABC向右平移7格,再向下平移2格,得到△![]() .(1)画出平移后的三角形;
.(1)画出平移后的三角形;
(2)若AB=5,则![]() = .
= .
(3)连接AA1,BB1, 根据“图形平移”的性质,得:线段AA1与线段BB1的数量关系和位置关系是: .
(4)求图中∠![]() AC+∠
AC+∠![]() BC的度数.
BC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红有4双完全相同的手套,都是左、右手不能换戴的,其中有两双是妈妈送的,一双是姑姑送的,另一双是同学送的,小红在这4双混放在一起的手套中任取两只,恰好是同学送的那双的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】万达旅行社为吸引市民组团去黄山风景区旅游,推出了如下的收费标准:

宿州高铁新区组织员工去黄山风景区旅游,共支付给万达旅行社旅游费用27 000元,请问该单位这次共有多少员工去黄山风景区旅游?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线MN与直线PQ垂直相交于O,点A在射线OP上运动,点B 在射线OM上运动.
(1)如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB的大小.
(2)如图2,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,AD、BC的延长线交于点F,点A、B在运动的过程中,∠F= °;DE、CE又分别是∠ADC和∠BCD的角平分线,点A、B在运动的过程中,∠CED的大小也不发生变化,其大小为∠CED= °.
(3)如图3,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及其延长线相交于E、F,则∠EAF= ° ;在△AEF中,如果有一个角是另一个角的3倍,则∠ABO= °.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个港口相距72千米,一艘轮船从甲港出发,顺流航行3小时到达乙港,休息1小时后立即返回;一艘快艇在轮船出发2小时后从乙港出发,逆流航行2小时到甲港,并立即返回(掉头时间忽略不计)。已知水流速度是2千米/时,下图表示轮船和快艇距甲港的距离y(千米)与轮船出发时间x(小时)之间的函数关系式,结合图象解答下列问题:
(顺流速度=船在静水中速度+水流速度;逆流速度=船在静水中速度-水流速度)

(1)轮船在静水中的速度是 千米/时;快艇在静水中的速度是 千米/时;
(2)求快艇返回时的解析式,写出自变量取值范围;
(3)快艇出发多长时间,轮船和快艇在返回途中相距12千米?(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E,∠ADC=70°.
(1)求∠EDC的度数;
(2)若∠ABC=n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示);若不改变,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com