
【题目】如图,在下列每个图形中(每个图形都各自独立),是否存在相似的三角形,如果存在,把它们用字母表示出来,并简要说明识别的根据.

【答案】详见解析.
【解析】试题分析:
(1)由图中信息可知,∠A=∠A,∠ADE=∠ABC,故△ADE∽△ABC;
(2)由图中信息可知,∠A=∠A,∠AED=∠ABC,故△ADE∽△ACB;
(3)由图中信息可知,∠C=∠C,∠CDE=∠CAB,故△CDE∽△CAB;
(4)由图中信息可知,∠AEB=∠CED,AE:CE=BE:DE=1:2,故△ABE∽△CDE;
(5)由图中信息可知,∠DAB=∠BAC,AB:AC=AD:AB=2:3,故△ABD∽△ACB;
(6)由图中信息可知,∠BAD=∠CAB,AD:AB=AB:AC=1:2,故△ABD∽△ACB;
试题解析:
(1)△ADE∽△ABC,理由如下:
由图中信息可知,∠A=∠A,∠ADE=∠ABC=50°,
∴△ADE∽△ABC;
(2)△ADE∽△ACB,理由如下:
由图中信息可知,∠A=∠A,∠AED=∠ABC=70°,
∴△ADE∽△ACB;
(3)△CDE∽△CAB,理由如下:
由图中信息可知,∠C=∠C,∠CDE=∠CAB=90°,
∴△CDE∽△CAB;
(4)△ADE∽△ACB,理由如下:
由图中信息可知,AE:CE=2:4=1:2,BE:DE=3:6=1:2,
∴AE:CE=BE:DE=1:2,
又∵∠AEB=∠CED,
∴△ABE∽△CDE.
(5)△ABD∽△ACB,理由如下:
由图中信息可知,AD:AB=4:6=2:3,AB:AC=6:9=2:3,
∴AD:AB=AB:AC=2:3,
又∵∠DAB=∠BAC,
∴△ABD∽△ACB.
(6)△ABD∽△ACB,理由如下:
由图中信息可知,AD:AB=2:4=1:2,AB:AC=4:8=1:2,
∴AD:AB=AB:AC,
又∵∠BAD=∠CAB,
∴△ABD∽△ACB.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,AB边上有一动点P,连接PD,线段PD绕点P顺时针旋转90°后,得到线段PE,且PE交BC于F,连接DF,过点E作EQ⊥AB的延长线于点Q.
(1)求线段PQ的长;
(2)问:点P在何处时,△PFD∽△BFP,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们生活水平的提高,家用轿车越来越多地进入家庭.王先生家中买了一辆小轿车,他连续记录了7天中每天行驶的路程(如下表),以50km为标准,多于50km的记为“+”,不足50km的记为“﹣”,刚好50km的记为“0”.
第一天 | 第二天 | 第三天 | 第四天 | 第五天 | 第六天 | 第七天 | |
路程(km) | ﹣8 | ﹣11 | ﹣14 | 0 | ﹣16 | +41 | +15 |
(1)王先生这七天中平均每天驾车行驶多少千米?
(2)若每行驶1km需用汽油0.1升,汽油价格为6.5元/升,则王先生家一个月(按30天计)的汽油费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:
(1)画出△ABC关于y轴的对称图形△A1B1C1;
(2)请计算△ABC的面积;
(3)直接写出△ABC关于x轴对称的三角形△A2B2C2的各点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你能化简(x﹣1)(x99+x98+…+…+x+1)吗?遇到这样的复杂问题时,我们可以先从简单的情形入手.然后归纳出一些方法.
(1)分别化简下列各式:
(x﹣1)(x+1)= ;
(x﹣1)(x2+x+1)= ;
(x﹣1)(x3+x2+x+1)= ;
…
(x﹣1)(x99+x98+…+x+1)= .
(2)请你利用上面的结论计算:
299+298+…+2+1
399+398+…+3+1
查看答案和解析>>
科目:初中数学 来源: 题型:
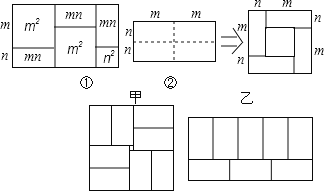
【题目】有许多代数恒等式可以用图形的面积来表示,如图①,它表示了(2m+n)(m+n)=2m2+3mn+n2.
(1)图②是将一个长2m、宽2n的长方形,沿图中虚线平方为四块小长方形,然后再拼成一个正方形,请你观察图形,写出三个代数式(m+n)2、(m-n)2、mn关系的等式: ;
(2)若已知x+y=7、xy=10,则(x-y) 2= ;
(3)小明用8个一样大的长方形(长acm,宽bcm)拼图,拼出了如图甲、乙的两种图案,图案甲是一个正方形,图案乙是一个大的长方形,图案甲的中间留下了边长是2cm的正方形小洞,则(a+2b)2-8ab的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC中,D为BC上一点,E为△ABC外部一点,DE交AC于一点O,AC=AE,AD=AB,∠BAC=∠DAE.
(1)求证:△ABC≌△ADE;
(2)若∠BAD=20°,求∠CDE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)请画出△ABC关于y轴对称的△A′B′C′(其中A′,B′,C′分别是A,B,C的对应点,不写画法);
(2)直接写出A′,B′,C′三点的坐标:A′( ),B′( ),C′( )
(3)计算△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在折纸活动中,小明制作了一张⊿ABC纸片,点D、E分别是边AB、AC上,将⊿ABC沿着DE折叠压平,A与A’重合,若∠A=75°,则∠1+∠2=( )
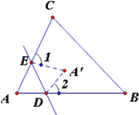
A. 150° B. 210° C. 105° D. 75°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com